Связь между решениями неоднородной системы линейных уравнений с решениями ассоциированной с ней однородной системы линейных уравнений

Лемма 1. Пусть (1) 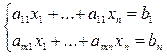- неоднородная система линейных уравнений над полем P, (2) 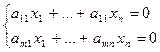- однородная система линейных уравнений, ассоциированная с (1). Тогда выполняются следующие условия:

1) Если 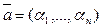и 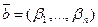- решения системы (1), то 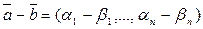- решение системы (2).

2) Если 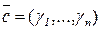- решение системы (1) и 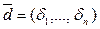- решение (2), то 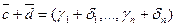- решение системы (1).

Доказательство. 1) Так как 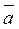- решение (1), то 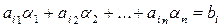. Так как 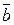- решение (1), то 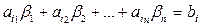. Тогда 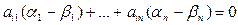, 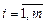=> 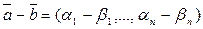- решение системы (2).

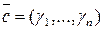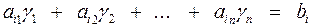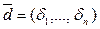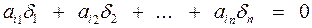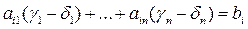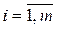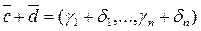2) Так как – решение системы (1), то . Так как – решение системы (2), то . Тогда , и - решение системы (1). Лемма доказана.

Теорема 1. Пусть (1) - неоднородная система линейных уравнений над полем P, (2) - однородная система линейных уравнений, ассоциированная с (1), Н – множество всех решений системы (1), U - множество всех решений системы (2), 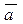- некоторое решение системы (1). Тогда Н =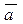+ U, где 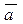+ U =.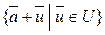

Из теоремы 1 следует, что для того, чтобы найти множество всех решений системы (1), достаточно найти множество всех решений системы (2) и хотя бы одно решение системы (1).