2014-02-09
1946
Прямой зависимости между проницаемостью и пористостью горных пород не существует. Например, трещиноватые известняки, имеющие малую пористость, часто обладают большой проницаемостью и, наоборот, глины, иногда характеризующиеся высокой пористостью, практически непроницаемы для жидкостей и газов, так как их поровое пространство слагается каналами субкапиллярного размера. Однако на основании среднестатистических данных можно сказать, что более проницаемые породы часто и более пористые.
Проницаемость пористой среды зависит преимущественно от размера поровых каналов, из которых слагается поровое пространство. Поэтому изучению структуры, строения и размеров пор уделяется большое внимание.
Зависимость проницаемости от размера пор можно получить путем приложения законов Дарси и Пуазейля к пористой среде, которую представим в виде системы трубок одинакового сечения. По закону Пуазейля расход Q жидкости через такую пористую среду составит
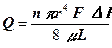, (1.12)
где n – число пор на единицу площади фильтрации; r – радиус порового канала; F – площадь фильтрации; ΔР – перепад давления; L – длина порового канала; μ – вязкость жидкости.
По определению коэффициент пористости среды, через которую проходит фильтрация, можно представить следующим образом:
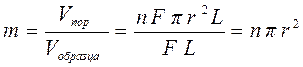(1.13)
Подставляя в формулу (1.12) вместо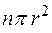 
значение пористости 
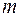получим
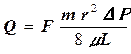(1.14)
Сравнивая полученное нами уравнение (1.14) с уравнением Дарси (Q = k•F•∆P/μ•L) и приравняв правые части этих уравнений, сократив подобные параметры, получим выражение для искомой взаимосвязи проницаемости, пористости и радиуса порового канала:
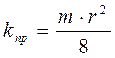(1.15)
Выражение (1.15) используется и для оценки радиуса (размера) порового канала для образцов кернового материала с известными величинами пористости и проницаемости:
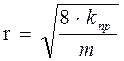. (1.16)
Уравнения (1.15 – 1.16) справедливы только для однородной пористой среды, например для кварцевого песка, и характеризуют взаимосвязь между пористостью, проницаемостью, радиусом порового канала. Для реальных коллекторов оценка радиуса порового канала производится с учётом структурных особенностей порового пространства пород. Обобщённым выражением для этих целей является, например, эмпирическое уравнение Ф. И. Котяхова:
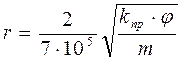(1.17)
где r – радиус пор; φ – структурный коэффициент, учитывающий извилистость порового пространства.
Величины φ оценивают экспериментально на модельных средах путём измерения электрического сопротивления пород. Как правило, значения коэффициентов φ обратно пропорциональны величинам коэффициентов пористости (m). По экспериментальным данным для керамических, пористых сред при изменении пористости от 0,39 до 0,28, коэффициент φ изменяется от 1,7 до 2,6.
