Чтобы обеспечить соответствующую основу для изучения структур данных следует обсудить существующие типы систем счислений: позиционные и непозиционные.
Непозиционные системы счисления
Числа используются для символического представления количества объектов. Очень простым методом представления количества является использование одинаковых значков. В такой системе между значками и пересчитываемыми объектами устанавливается взаимно однозначное соответствие. Например, шесть объектов могут быть представлены как ****** или 111111. Такая система становится очень неудобной, если попытаться с ее помощью представить большое количество объектов.
Системы счисления, подобные римской, обеспечивают частичное решение проблемы представления большого количества объектов. В римской системе дополнительные символы служат для представления групп значков. Например, если принять, что I=*, Y=IIIII, X=YY, L=XXXXX и т.д. Заданная величина представляется с помощью комбинирования символов в соответствии с рядом правил, которые в некоторой степени зависят от положения символа в числе. Недостатком системы, которая с самого начала основывается на группировании некоторого множества символов с целью формирования нового символа, является то обстоятельство, что для представления очень больших количеств требуется очень много уникальных символов.
Позиционные системы счисления
В позиционной системе счисления используется конечное число R уникальных символов. Величину R часто называют основанием системы счисления. В позиционной системе количество представляется как самими символами, так и их позицией в записи числа. Система счисления с основанием десять, или десятичная система является позиционной. Рассмотрим, например, число 1303. Его можно представить в виде:
1*103 + 3*102 + 0*101 + 3*100.
В позиционной системе могут быть представлены и дробные числа. Например, одна четвертая записывается в виде 0.25, что интерпретируется как:
2*10-1 + 5*10-2.
Другой пример позиционной системы счисления - двоичная система. Двоичное число 11001.101 представляет то же самое количество, что и десятичное число 26.625. Разложение данного двоичного числа в соответствии с его позиционным представлением следующее:
1*24+1*23+0*21+1*20 +1*2-1+0*2-2+1*2-3 =16+8+1+0.5+0.125 =26.625.
Наиболее часто встречаются системы счисления, имеющие основание 2,8,10 и 16, которые обычно называют двоичной, восьмеричной, десятичной и шестнадцатеричной системами, соответственно. Вся вычислительная техника работает в двоичной системе счисления, так как базовые элементы вычислительной техники имеют два устойчивых состояния. Восьмеричная и шестнадцатеричная системы используются для удобства работы с большими двоичными числами.
1.3.3 Изображение чисел в позиционной системе счисления
Изображение чисел в любой позиционной системе счисления с натуральным основанием R (R >1) базируется на представлении их в виде произведения целочисленной степени m основания R на полином от этого основания:
Ar = Rm * 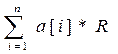
где: a[i] { 0,1,..., R-1 } - цифры R- ичной системы счисления;
n - количество разрядов (разрядность), используемых для представления числа;
R - основание системы счисления;
m {..., -2, -1, 0,+1,+2,...} - порядок числа;
R-1 - позиционный вес i - го разряда числа.
Так в десятичной (R=10) системе для представления чисел используются цифры a=(0,1,...9); в двоичной (R=2) - a=(0,1), в шестнадцатеричной (R=16), a=(0,1....9,A,B,C,D,E,F), где прописные латинские буквы A..F эквивалентны соответственно числам 10..15 в десятичной системе. Например,
1) 815=103*(8*10-1+1*10-2+5*10-3)=8*102+1*101+5*100;
2) 8.15=101*(8*10-1+1*10-2+5*10-3)=8*100+1*10-1+5*10-2;
3) 0.0815= 10-1*(8*10-1+1*10-2+5*10-3)=8*10-2+1*10-3+5*10-4.
Перевод чисел из одной системы счисления в другую
При переводе целого числа (целой части числа) из одной системы счисления в другую исходное число (или целую часть) надо разделить на основание системы счисления, в которую выполняется перевод. Деление выполнять, пока частное не станет меньше основания новой системы счисления. Результат перевода определяется остатками от деления: первый остаток дает младшую цифру результирующего числа, последнее частное от деления дает старшую цифру.
При переводе правильной дроби из одной системы счисления в другую систему счисления дробь следует умножать на основание системы счисления, в которую выполняется перевод. Полученная после первого умножения целая часть является старшим разрядом результирующего числа. Умножение вести до тех пор пока произведение станет равным нулю или будет получено требуемое число знаков после разделительной точки.
Например,
1) Перевести дробное число 0.243 из десятичной системы счисления в двоичную.
0.24310 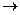 0.00111112.
0.00111112.
Проверка: 0.0011111 = 0*2-1+0*2-2+1*2-3+1*2-4+1*2-5+1*2-6+1*2-7= 0,2421875
2) Перевести целое число 164 из десятичной системы счисления в двоичную систему.
16410 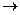 101001002
101001002
Проверка: 10100100 = 1*27+0*26+1*25+0*24+0*23+1*22+0*21+0*20= =128+32+4=164
При переводе смешанных чисел целая и дробная части числа переводятся отдельно.
 2014-02-24
2014-02-24 627
627








