Интуитивные методы прогнозирования (методы экспертных оценок)

Основная идея прогнозирования на основе экспертных оценок заключается в построении рациональной процедуры интуитивно-логического мышления человека в сочетании с количественными методами оценки и обработки получаемых результатов.

Сущность методов экспертных оценок заключается в том, что в основу прогноза закладывается мнение специалиста или коллектива специалистов, основанное на профессиональном, научном, практическом опыте.

Различают индивидуальные и коллективные экспертные оценки.

Индивидуальные экспертные оценки. Наиболее широкое распространение получили: метод интервью, аналитический метод;

Метод интервью предполагает беседу прогнозиста с экспертом по схеме «вопрос-ответ», в процессе которого прогнозист ставит в соответствии с заранее разработанной программой перед экспертом вопросы относительно перспектив развития прогнозируемого объекта. Успех данной оценки зависит от способности эксперта давать заключения по самым различным вопросам.

Аналитический метод предусматривает тщательную самостоятельную работу эксперта над анализом тенденций, оценкой состояния и путей развития прогнозируемого объекта. Свои выводы эксперт оформляет в виде докладной

записки. Основным преимуществом этого метода является возможность максимального использования индивидуальных особенностей эксперта. Однако он мало пригоден для прогнозирования сложных систем.

Методы коллективных экспертных оценок. Эти методы предполагают определение согласованности мнений экспертов по перспективным направлениям развития объектов прогнозирования, сформированными отдельными специалистами. В современных условиях используется математико-статистический инструментарий для обработки результатов опроса экспертов. Например, для оценки степени согласованности мнений экспертов исчисляются: дисперсия оценок, среднеквадратическое отклонение оценок, на этой основе рассчитывается коэффициент вариации оценок.

Метод коллективной генерации идей (метод мозговой атаки). Впервые был разработан в конце 30-ых годов 20 века американцем А. Осборном. Сущность метода состоит в использовании творческого потенциала специалистов при «мозговой атаке» проблемной ситуации, реализующей вначале генерацию идей и последующее деструктурирование (разрушение, критика) этих идей с формулированием контридей и выработке согласованной точки зрения.

Этот метод предполагает реализацию следующих этапов:

1 этап: формирование группы участников (по численности и по составу), наиболее продуктивные группы 10-15 человек;

2 этап: составляется проблемная записка, она формируется группой анализа и включает описание метода и проблемной ситуации;

3 этап: генерация идей. Каждый участник имеет право выступать много раз, критика выступающего на данном этапе не допускается;

4 этап: систематизация идей, высказанных на этапе генерации;

5 этап: деструктурирование систематизированных идей (каждая идея
подвергается критике со стороны группы высококвалифицированных
специалистов, группа формируется в кол-ве 20-25 человек);

6 этап: дается оценка критических замечаний и составляется список практически
реализуемых идей.

Этот метод позволяет качественно и быстро проводить оценку вариантов развития прогнозируемых объектов.

Метод «635» - одна из разновидностей «мозговой атаки». 6 - означает шесть участников, каждый из которых должен записать 3 идеи в течение 5 минут. Лист ходит по кругу, т.о. за полчаса каждый запишет в свой актив 18 идей, в общей сложности 108 идей. Структура идей четко определена. Этот метод широко используется в зарубежных странах, особенно в Японии, для отбора из множества идей наиболее оригинальных и прогрессивных.

Метод «Делъфи» разработанный американской корпорацией РЭНД (Т.Гордоном и О.Хелмером) в 1964г. и получивший название от города Дельфы, который был известен в Древней Греции благодаря своим прорицателям-оракулам. Метод представляет собой обобщение оценок экспертов, касающихся перспектив развития того или иного экономического объекта. Особенность метода состоит в последовательном, индивидуальном анонимном опросе экспертов. Прогнозирование с помощью этого метода проводиться в несколько туров, результаты обрабатываются статистическими методами.

1 тур: среди экспертов проводиться опрос, затем экспертов знакомят со средним значением и разницей между крайними значениями оценок или со всей совокупностью, сохраняя анонимность.

2 тур: вторичный анонимный опрос, перед которым экспертов, чьи оценки сильно отклоняются от среднего значения, просят аргументировать свои оценки.

3 тур: знакомят с оценками 2 тура, включая аргументы крайних значений оценок, просят рассмотреть новые оценки и их обоснование и пересмотреть свои оценки.

В результате вырабатывается согласованное суждение перспектив развития объекта.

Метод комиссий основан на работе специальных комиссий. Группы экспертов за «круглым столом» обсуждают ту или иную проблему с целью выработки единого мнения. Недостаток этого метода заключается в том, что группа экспертов в своих суждениях руководствуется в основном логикой компромисса.

Вывод: Для надежности экспертных оценок нужно выполнение по крайней мере 2-х условий:

• наличие высококвалифицированных экспертов

• обеспечение объективности, независимости их мнений.

Метод написания сценария можно отнести как к индивидуальным, так и коллективным экспертным оценкам. Он основан на определении логики процесса или явления во времени при различных условиях.

Сценарий - это модель будущего, в котором описывается возможный ход событий с указанием вероятностей их реализации. Прогнозный сценарий определяет стратегия развития прогнозируемого объекта, приоритеты проблем и ресурсы для достижения основных целей. Он обычно носит многовариантный характер и рассматривает 3 линии поведения:

1. оптимистическую: развитие объекта в благоприятной ситуации;

2. пессимистическую: развитие системы, объекта в наименее благоприятной ситуации;

3. рабочую: развитие системы с учетом противодействия отрицательных факторов, проявление которых наиболее вероятно.

Метод подготовки сценариев вначале использовался для выявления возможных результатов военных действий, сейчас все чаще применяется в экономической политике и в стратегическом корпоративном планировании.

Использование сценарного прогнозирования в условиях рынка обеспечивает:

- лучшее понимание ситуации, ее эволюции;

- оценку потенциальных угроз;

- выявление благоприятных возможностей;

- выявление возможных и целесообразных направлений деятельности;

- повышение уровня адаптации к изменениям внешней среды.

2 Формализованные методы прогнозирования:

2.1 Методы экстраполяции.

Методы экстраполяции являются наиболее распространенными и проработанными. Сущность экстраполяции заключается в изучении сложившихся в прошлом и настоящем устойчивых тенденций развития объекта прогноза и переносе их на будущее. В экономическом прогнозировании широко применяется метод математической экстраполяции, в математическом смысле это распространение закона изменения функции из области ее наблюдения на область, лежащую вне отрезка наблюдения.

Функция представляет простейшую математико-статистическую модель, отражающую зависимость объекта прогнозирования (экономического показателя) от влияющих на него факторов. В качестве факторов могут выступать различные показатели, а также время (номер периода).

Методы экстраполяции необходимо применять на начальном этапе прогнозирования для выявления тенденций, а также при стабильности системы, устойчивости явлений, когда динамика процессов, показателей в перспективе определяется тенденциями их изменения в прошедшем периоде. Нужно иметь информацию об устойчивости тенденций за срок, в 2 - 3 раза превышающий срок прогнозирования.

2.1.1 Метод подбора функций – один из распространенных методов экстраполяции. Главным этапом экстраполяции тренда является выбор оптимального вида функции, описывающей эмпирический ряд. Для этого проводятся предварительная обработка и преобразование исходных данных с целью облегчения выбора вида зависимости путем сглаживания и выравнивания временного ряда.

Динамический или временной ряд – это совокупность значений изучаемого показателя, относящихся к некоторым последовательным интервалам или моментам времени (эмпирический ряд – это совокупность наблюдений, упорядоченных во времени).

Тренд – это тенденция описания некоторой функции от времени, это длительная тенденция изменения экономических показателей.

Прогноз методом подбора функций предполагает продление тенденции прошлого, выражаемой выбранной функцией, в будущее, т.е. экстраполяцию динамического ряда.

Задача выбора функции заключается в подборе по фактическим данным (x_i;y_i) формы зависимости (линии) y=f(t), так чтобы отклонения ∆ _i данных исходного ряда y_i от соответствующих расчетных у_i находящихся на линии, были наименьшими. После этого линию можно продолжить (экстраполировать) и получить прогноз. На практике выбор вида функции осуществляется на основе графика.

В случае линейной зависимости уравнение имеет вид у = а + bх. Расчет параметров а, b для конкретной функциональной зависимости осуществляется с помощью метода наименьших квадратов (МНК) и его модификаций. Суть МНК состоит в отыскании параметров модели, минимизирующих отклонения расчетных значений от соответствующих значений эмпирического ряда, т.е. искомые параметры должны удовлетворять условию

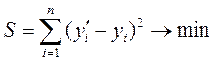
где п - число наблюдений в эмпирическом ряду.

Расчет значений параметров зависимости осуществляется путем решения системы нормальных уравнений, получаемой дифференцированием функции S по а и b.

В случае однофакторной линейной зависимости у = а + вх она имеет вид:

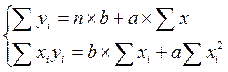
Выбор модели осуществляется с помощью специально разработанных программ. Есть программы, предусматривающие возможность моделирования экономических рядов по 16 функциям: линейной, гиперболической различных типов, экспоненциальной, степенной, логарифмической и др. Каждая из них может иметь, свою специфическую область применения при прогнозировании экономических явлений.

Из трендовых моделей в прогнозировании спроса наиболее широко используются следующие виды:

а) уравнение прямой у = а + bх

б) логарифмической у = а + b lgx

в) гиперболическая функция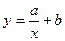

г) экспоненциальная функция у = а^х

д) параболическая функция у = а +bх + cх

Так, линейная функция у = а +bх применяется для описания процессов, равномерно развивающихся во времени. Гиперболы хорошо описывают процессы, характеризующиеся насыщением, когда существует фактор, сдерживающий изменение прогнозируемого показателя.

В связи с тем, что метод подбора функций исходит из инерционности экономических явлений и предпосылок, что общие условия, определяющие развитие в прошлом, не претерпят существенных изменений в будущем, его целесообразно использовать при разработке краткосрочных прогнозов обязательно в сочетании с методами экспертных оценок.

Экстраполяция методом подбора функций учитывает все данные исходного ряда с одинаковым «весом». Классический метод наименьших квадратов предполагает равноценность исходной информации в модели. Однако, как показывает опыт, экономические показатели имеют тенденцию «старения». Влияние более поздних наблюдений на развитие процесса в будущем существеннее, чем более ранних. Проблему «старения» данных динамических рядов решает метод экспоненциального сглаживания с регулируемым трендом.

5.1.2 Метод экспоненциального сглаживания с регулируемым трендом. Прогноз при экспоненциальном сглаживании определяется как сумма фактических и прогнозных данных за период, взвешенных с помощью специальных коэффициентов, определяемых статистическим путем.

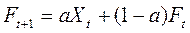
где F_t+1 - прогноз продаж на месяц t+1;

X_t - продажи в месяце t (фактические данные);

F_t - прогноз продаж на месяц t;

а - специальный коэффициент, параметр сглаживания, определяемый статистическим путем..

Метод позволяет построить такое описание процесса, при котором более поздним наблюдениям придаются большие «веса» по сравнению с более ранними, причем «веса» наблюдений убывают по экспоненте. В результате создается возможность получить оценку параметров зависимости, характеризующих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения.

Скорость старения данных характеризует параметр сглаживания а. Он изменяется в пределах 0 < а < 1. В зависимости от величины параметра прогнозные оценки по-разному учитывают влияние исходного ряда наблюдений: чем больше а, тем больше вклад последних наблюдений в формирование зависимости, а влияние начальных условий быстро убывает. При малом а прогнозные оценки учитывают все наблюдения, при этом уменьшение влияния более «старой» информации происходит медленно, т.е. чем меньше а, тем данные более стабильны, и наоборот.

В области экономического прогнозирования наиболее употребимы пределы 0,05 < а < 0,3. Значение а в общем случае должно зависеть от срока прогнозирования: чем меньше срок, тем большим должно быть значение параметра.

Пример: В таблице приведены фактические и прогнозные данные об объеме производства услуг фирмы по ремонту и пошиву одежды за 7 лет (в тыс. руб.)

Год	Объем производства услуг по факту	Объем производства услуг по прогнозу

Требуется дать прогнозную оценку объема производства услуг фирмы на 2010 г.

Предположим, что коэффициент а для прогноза на 2010 год а = 0,2.

Прогноз объема производства услуг на 2010 год составит:

F₀₁₀ = 0,2 * 625 + (1 - 0,2) * 620 = 621 тыс. руб.

5.1.3 Метод скользящего среднего предполагает, что следующий по времени показатель по своей величине равен средней за последние месяцы (годы) величине, например средней за последние 3 года:

Прогноз на 2010 = (575+600+625)/3=598 тыс. руб

5.2 Экономико-математические методы. Сущность и содержание экономико-математического моделирования в планировании финансовых показателей заключаются в том, что оно позволяет найти количественное выражение взаимосвязей между финансовыми показателями и факторами, их определяющими. Эта связь выражается через экономико-математическую модель. Экономико-математическая модель представляет собой точное математическое описание экономического процесса, т.е. описание факторов, характеризующих структуру и закономерности изменения данного экономического явления с помощью математических символов и приемов (уравнений, неравенств, таблиц, графиков и т. д.). В модель включаются только основные (определяющие) факторы.

Модель может строиться по функциональной или корреляционной связи. Функциональная связь выражается уравнением вида:

Y = f (х), где Y - показатель; х - факторы.

Корреляционная связь – это вероятностная зависимость, которая проявляется лишь в общем и только при большом количестве наблюдения. Корреляционная связь выражается уравнениями регрессии различного вида. Например, однофакторные модели вида:

линейного Y = а₀ + а₁ Х;

параболы Y = а₀ + а₁ Х + а₂Х²

гиперболы Y =а₀ + а₁ Х а₁ / Х

многофакторные модели вида:

линейного у = а₀ + а,Х +... + аn Xn.

логарифмического log Y = а₀ + a₁ log Х₁... а_n log Х_n,

где а₀ - а₁ -...- а_n - параметры уравнения и т. п.

При расчете моделей планирования первостепенное значение имеет определение периода исследования. Он должен браться таким, чтобы исходные данные были бы однородны. При этом следует иметь в виду, что слишком малый период исследования не позволяет выявить общие закономерности. С другой стороны, нельзя брать и слишком большой период, так как любые экономические закономерности непостоянны и могут существенно изменяться в течение длительного времени. В связи с этим при практической плановой работе наиболее целесообразно использовать для перспективного планирования годовые данные финансовой деятельности за 5 лет, а для текущего (годового) планирования - квартальные данные за 1-2 года. При существенных изменениях условий работы хозяйствующего субъекта в плановом периоде в рассчитанные на основе экономико-математических моделей показатели вносятся необходимые коррективы. Экономико-математическое моделирование позволяет также перейти в планировании от средних величин к оптимальным вариантам.

В экономико-математическую модель должны включаться не все, а только основные факторы. Проверка качества моделей производится практикой. Практика применения моделей показывает, что сложные модели со множеством параметров оказываются зачастую непригодными для практического использования

Пример. Экономико-математическая модель зависимости суммы прибыли от объема выручки выражается линейным управлением вида

Y = а₀ + а₁ Х,

где Y - прибыль, руб.;

Х - выручка, руб.;

а₀, а₁ - параметры уравнения;

а₁ - коэффициент регрессии, показывающий, на сколько рублей увеличивается прибыль при увеличении выручки на один рубль;

а₀ - сумма прибыли, определяемая совокупным действием всех других факторов, кроме выручки, руб.

Решение модели заключается в нахождении параметров а₀ и а₁. Эти параметры обычно отыскиваются методом наименьших квадратов.

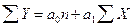
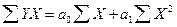
Важное значение для обоснованности модели имеет ее репрезентативность. Репрезентативность наблюдений - это показательность наблюдений, т. е. речь идет о соответствии характеристик, полученных в результате частичного обследования объекта, характеристикам этого объекта в целом. Репрезентативность полученных показателей модели проверяется путем расчетов среднего квадратического отклонения полученных данных от фактических и коэффициента вариации. Среднее квадратическое отклонение определяется по формуле

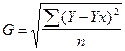
где G - среднее квадратическое отклонение;

Y - фактическая сумма прибыли, руб.;

Y x - расчетная сумма прибыли, руб.;

n - число случаев наблюдений.

Коэффициент вариации (V) представляет собой процентное отношение среднего квадратического отклонения к среднеарифметической величине отчетных (фактических) показателей.

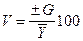
где V - коэффициент вариации, %;

G-среднее квадратическое отклонение, руб.;

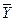- среднеарифметическая величина прибыли, руб.

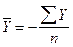
Расчет экономико-математической модели зависимости прибыли от выручки приведен в табл. 3.

Таблица 3

Расчет экономико-математической модели зависимости прибыли от выручки

Кварталы	Прибыль, млн. руб. Y	Выручка,млн. руб. X	Y X	X2	Расчетная прибыль Y x	Y - Yx	(Y - Yx)2
I	4,1		73,8		4,3	-0,2	0,04
II	4,5		94,5		4,5	--	--
III	4,2		80,8		4,4	-0,2	0,04
IV	5,2		135,2		4,8	+0,4	0,16
Итого			384,3				0,24

По данным табл. 22 система нормальных уравнений для нахождения параметров а₀ и а₁ имеет вид:

18 = а₀ 4 + а₁ 85; (1)

384,3 = а₀ 85 + а₁ 1841 (2)

Находим параметр а₀ из первого уравнения

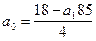
и подставляем его во второе уравнение

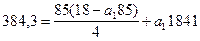
384,3 = 382,5 - а₁ 1806,25 + а₁ 1841

1,8 = 34,75 а₁

а₁ = 1,8 / 34,75 = 0,05

а₀ = (18 - 0,05 * 85) / 4 = 3,4

Таким образом, модель имеет вид:

Yх = 3,4 + 0,052 X,

где параметр а₁ = 0,052 показывает, что при увеличении выручки на 1 руб. прибыль возрастает на 0,052 руб.;

параметр а₀ = 3,4 показывает среднюю сумму прибыли (3,4 млн. руб.), которая определяется действиями всех других факторов, кроме выручки.

Подставляя в модель значения Х для каждого квартала, определяем значение Y для каждого квартала.

Например, Y₁ = 3,4 + 0,05 * 18 = 4,3 млн. руб.

Среднее квадратическое отклонение составляет

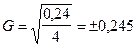
Коэффициент вариации

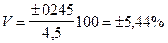
Y = 18 / 4 = 4,5 млн. руб.

Коэффициент вариации показывает, что степень отклонения расчетных показателей от фактических составляет всего лишь 5,44%, т. е. незначительная. Поэтому можно сделать вывод о возможности использования данной модели при планировании прибыли.

Так, на плановый квартал планируется сумма выручки в размере 32 млн. руб. Тогда план прибыли должен составить Y_план = 3,4 + 0,05 * 32 = 5 млн. руб.

Регрессионный анализ как разновидность статистического исследования использует набор коэффициентов, характеризующих точность и надежность полученного результата. К ним относятся:

1. Коэффициент корреляции r показывает степень корреляции (зависимости) между значениями X и Y и определяется по формуле:

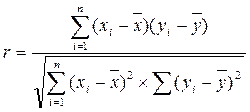
Значение коэффициента корреляции изменяется в интервале [-1,1]

Если значение:

г = -1 свидетельствует о наличии обратно пропорциональной связи между изучаемыми признаками:

г = +1 - функциональная прямо пропорциональная зависимость,

г близко к 0 предполагает отсутствие линейной связи между признаками.

На практике: при [г]< 0,3 - связь слабая

при 0,3 < [г] < 0,7 - связь средней тесноты

при [г] > 0,7 - тесная связь.

Более широко используется коэффициент смешанной корреляции (коэффициент детерминации) г₂, который говорит о том, насколько хорошо составлено уравнение регрессии. Если говорить точнее, этот коэффициент характеризует "добротность" модели предсказания (в какой степени совпадают фактические и прогнозируемые значения Y). Чем больше значение R₂, тем лучше. R₂ изменяется в диапазоне [0,1].

Коэффициент детерминации

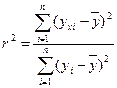
Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (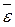) называемого средней ошибкой аппроксимизации. Рекомендуемое значение для 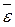< 15%.

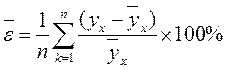
Авторегрессионные модели. На практике также нередко используют модификацию уравнения 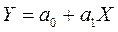, вводя в него в качестве фактора период (момент) времени t. Тогда уравнение будет иметь вид:

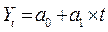
Пример: Уравнение прямой линии выражено формулой: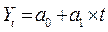

Для нахождения параметров а₀ и а₁, необходимо решить систему нормальных уравнений:

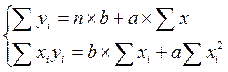
где у - фактические уровни ряда динамики;

n - число уровней.

Для упрощения расчетов обозначим время так, чтобы начало отсчета времени приходилось на середину рассматриваемого периода.

Данные для расчета параметров а₀ и а₁ представлены во вспомогательной таблице:

Годы
Т	-3	-2	-1		+1	+2	+3

Следовательно, 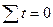, тогда система нормальных уравнений примет вид:

Данные для расчета параметров а₀ и а_х представлены во вспомогательной таблице:

годы	Фактические объемы производства т.р. Y	Условные годы, t	t2	y*t	yt
		-3		-1380
		-2		-940
		-1		-500
∑

a₀ = 536,43 a₁= 29,46.

Таким образом, уравнение прямой примет вид:

Y_t =536,43 + 29,46 t

Подставив в это уравнение значение t (гр.З), получим выровненные теоретические значения Y_t (гр.6).

Условное значение 2008 г. будет (+4). Исходя из этого, определим прогноз объема производства услуг на 2008 г.:

У₂₀₀₈ = 536,43 + 29,46* 4 = 654,3 тыс. руб.

Для характеристики адекватности уравнения авторегрессионной зависимости используют величину среднего относительного линейного отклонения.

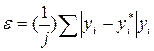
где 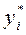- расчетная величина показателя У в момент времени i;

у_i - фактическая величина показателя У в момент времени i.

Если е < 0,15, считается, что уравнение авторегрессии может использоваться при определении тренда временного ряда экономического показателя в прогнозных целях. Ввиду простоты расчета критерий е достаточно часто применяется при построении регрессионных моделей. Если его значение не превышает 15%, то считается, что уравнение авторегрессии может использоваться в прогнозных целях.