Термодинамические условия устойчивости систем к флуктуациям. Б) Некристаллизующиеся бинарные системы (растворы, смеси)

Г) Механизм Киббла-Зурека

В) Блоксополимеры

Б) Некристаллизующиеся бинарные системы (растворы, смеси).

К этим системам относятся, в первую очередь, растворы трудно кристаллизующихся органических жидкостей и смеси (растворы) расплавов некристаллизующихся термопластичных полимеров друг с другом или другими нелетучими некристаллизующимися компонентами. Важнейшей особенностью таких систем, при заданном давлении, является ограниченная растворимость (термодинамическая совместимость) компонентов в аморфном состоянии и неспособность кристаллизоваться при температуре ниже Т_m вследствие кинетических и молекулярных структурных (стерических) эффектов. Вследствие ограниченной термодинамической совместимости компонен­тов, определяемой молекулярной массой и характером межмолекулярного взаимодействия при заданных параметрах состояния (температуре, давлении и составе), эти композиции могут находиться в гомогенном однофазном состоянии (в виде раствора) только при достаточно высокой температуре и малом содержании одного из компонентов. Для обобщенной характеристики равновесного фазового состояния таких систем с учетом термодинамической совместимости компонентов используют зависимости избыточной (по отношению к стандартному состоянию – чистым компонентам) мольной свободной энергии смешения или избыточных значений химических потенциалов компонентов от их мольных (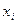) или объемных (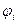) долей при заданных температуре и давлении, из которых получают диаграммы состояния в координатах температура-состав. Диаграммы сос­тоят из двух линий - бинодали и спинодали, разделяющих области равновесного, термодинамически стабильного однофазного (выше бинодали) и нестабильного, или двухфазного (ниже спинодали) состояний с полной и ограниченной совместимостью компонентов соответственно. Области между бинодалью и спинодалью характеризуют метастабильное, термодинамически неустойчивое состояние. При Т>ВКТР эта область исчезает. Теоретическое построение таких диаграмм базируется на статистической теории растворов полимеров Флори-Хаггинса, позволяющей рассчитывать избыточные значения плотности средней сво­бодной энергии смешения, т.е. величины, приходящейся на единицу объема (Δg_см) в зависимости от температуры и природы компонентов (молекулярной массы и межмолекулярного взаимодействия). Ее первые производные по числу молекул или звеньев цепей полимеров, соответствуют избыточным значениям химических потенциалов компонентов (Δμ₁ и Δμ₂). Равенство Δμ₁ и Δμ₂ характеризует равновесное сосуществование аморфного гомогенного и гетерогенного состояний, т.е дает линию бинодали. Вторые производные плотности средней сво­бодной энергии смешения по составу характеризуют границу метастабильной области (спинодаль), а третьи – верхнюю критическую точку растворимости компонентов.

Наибольший вклад в свободную энергию смешения и химические потенциалы некристаллизующихся компонентов в смеси дает комбинаториальная энтропия смешения ΔS_см, а особенности межмолекулярного взаимодействия компонентов учитывается через парный парамет­р взаимодействия 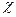, характеризующий изменение энергии при разрыве связей между молекулами исходных компонентов 1-1 (ω₁₁) и 2-2 (ω₂₂) и образования связей их друг с другом 1-2 (ω₁₂): 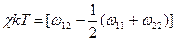, где k –константа Больцмана; Т – абсолютная температура. В усовершенствованных теориях параметр χ рассматривают состоящим из энтальпийного (χ_H) и энтропийного некомбинаториального (χ_S) вкладов: χ = χ_H + χ_S. В идеальных, или θ -условиях χ_H =0, а χ_S =1/2. Полуэмпирическим методов параметр χ может быть рассчитан через разность параметров растворимости компонентов Δδ= δ₁- δ₂, которые представляют собой корни квадратные из плотности энергии когезии е _к: 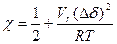, где V_r – средний мольный объем повторяющихся звеньев компонентов. Значения параметров растворимости компонентов могут быть рассчитаны непосредственно или через мольную энергии когезии по вкладам групп или другими методами. Предложено также эмпирическое соотношение, описывающее зависимость параметра взаимодействия от состава смеси и температуры: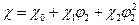, где 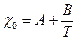, χ₁, χ₂, А, В - константы, учитывающие молекулярную массу и полидисперсность компонентов и другие эффекты.

Обобщенные выражения для плотности энергии смешения (Δg_см) и химических потенциалов компонентов с линейной формой макромолекул в бинарной смеси как первых производных Δg_см по составу: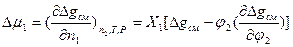, 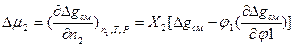в соответствие с теорией Флори-Хаггинса записываются в следующем виде соответственно: ;

; ,

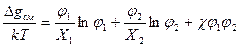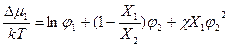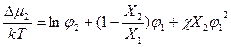где n₁, n₂, Х₁, Х₂ – число молекул и степени полимеризации компонентов соответственно: n₁Х₁, n₂Х₂ – общее количество повторяющихся звеньев полимерных компонентов (в случае, если один компонентов низкомолекулярный N₁ =1); φ₁, φ₂ – объемные доли компонентов. При примерно равных объемах звеньев компонентов: .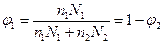

Линия бинодали соответствует точкам минимума на кривых зависимостей Δg_см от состава смеси при различных температурах и, соответственно, уравнения бинодали составляются из условий равенства химических потенциалов компонентов в различных фазах. Число уравнений, которые должны быть одновременно решены для построения линии бинодали на фазовой диаграмме, в соответствие с правилом фаз Гиббса, равно: У=К(Ф-1), где К – число компонентов, Ф – максимальное число сосуществующих фаз. Для сосуществующих фаз, являющихся только аморфными, не способными переходить в парообразное и кристаллическое состояние как в случае некристаллизующихся полимерных композиций, максимальное их число равно числу компонентов в смеси вне зависимости от температуры и давления. Поэтому для таких композиций число уравнений, которые должны быть решены одновременно, равно числу компонентов, т.е. для бинарных систем должны быть решены два уравнения для двух сосуществующих фаз (I и II): Δ μ₁^I= Δ μ₁ ^II иΔ μ₂^I= Δ μ₂^II, ил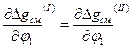и и .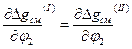

Линия спинодали соответствует точкам перегиба на кривых зависимостей Δg_см от состава смеси при различных температурах, а уравнение спинодали соответствует равенству нулю второй производной свободной энергии смешения по составу:

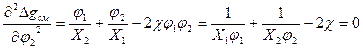. Если принять, что χ есть функция только температуры (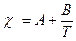), то, то уравнение спинодали в терминах температуры как функции состава принимает вид: .

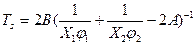На рис.4 приведены расчетные диаграммы состояния смеси низкомолекулярного (N₁=1) и высокомолекулярного компонента с различной степенью полимеризации при .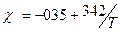

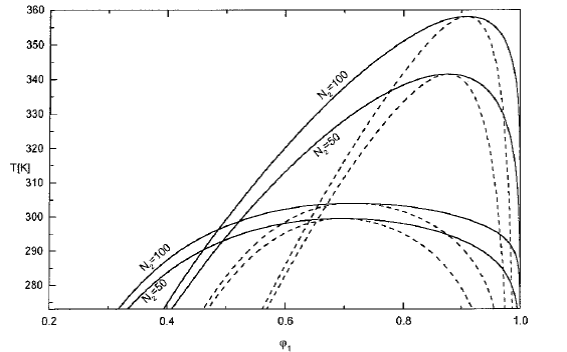
Рис.4. Расчетные диаграммы состояния смеси низкомолекулярного (N ₁=1) и высокомолекулярного компонента с различной степенью полимеризации пр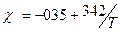и и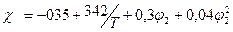

Во всех случаях диаграммы имеют верхнюю критическую точку, где сходятся бинодаль и спинодаль, координаты которой (Т_кр или χ_кр и φ_кр) определяются решением системы уравнени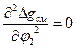й: и 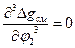. Для параметров критической точки получены сравнительно простые выражения: 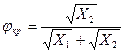; ; 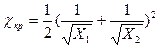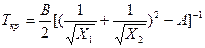. Для бинарной системы, компоненты которой имеют равные степени полимеризации и мольные объемы повторяющихся звеньев: Х=Х₁=Х₂, V=V₁=V₂) фазовая диаграмма симметрична, причем φ_кр =1/2, а χ_кр=2/Х. Чем больше Х₂ превышает Х₁, тем более ассиметричной становится фазовая диаграмма со смещением верхней критической точки в сторону повышенной концентрации низкомолекулярного компонента.

Если один из компонентов (второй) – сетчатый полимер, то в общее изменение плотности свободной энергии при его набухании в низкомолекулярном компоненте свой вклад вносит не только молекулярное перемешивание (Δg_см), но и упругое сопротивление сетки увеличению ее объема (Δg_упр). Сумма этих компонентов рамках классической теории набухания сетчатых полимеров Флори-Ренера в равновесных условиях дает следующее выражение для общей Δg:

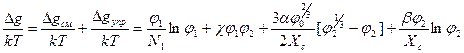, где φ₀ – константа, величина которой лежит между 0 и 1 (при формировании полимерной сетки непосредственно в присутствии первого компонента φ₀=φ₂); Х _c – степень полимеризации цепей сетчатого полимера между узлами сетки; α и β – параметры упругости полимерной сетки (по теории Флори-Ренера α=1 и β=2/ f, где f – функциональность узлов сетки, т.е. число сходящихся в них цепей. В усовершенствованных теориях α и β являются функциями объемной доли сетчатого полимера и функциональности узлов сетк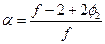и: и .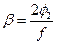

При очень быстром переходе из однофазной стабильной области в нестабильную гетерофазную через метастабильую область (за время меньше времени жизни флуктуаций концентрации) или напрямую через верхнюю критическую точку процесс фазового разделения бинарных растворов на начальной стадии протекает по механизму критического, или спинодального распада системы на две аморфные фазы в результате критического (безактивационного) роста всех флуктуаций концентрации (возрастания их амплитуды), кинетика которого в решающей степени определяется диффузионными эффектами. Такой механизм разделения фаз обусловлен формой кривой зависимости плотности свободной энергии смешения в нестабильной области между точками перегиба. В отличие от метастабильных областей между точками минимумов и перегибов, где участки кривой являются вогнутыми и более крутыми в сторону точек перегиба, чем точек минимума, в нестабильной области кривая является выпуклой и более крутой в сторону точек перегиба, чем точки максимума. Соответственно, в метастабильных областях любые одинаковые отклонения концентрации от среднего значения сопровождаются меньшим уменьшением свободной энергии при отклонении в сторону точки минимума, чем ее возрастанием при отклонении в сторону точки перегиба, т.е. любые флуктуации концентрации при этом, если они не превысят некоторого критического, достаточно большого размера, когда начинает превалировать выигрыш в свободной поверхностной энергии, приводят к возрастанию свободной энергии и гасятся (демпфируют). В нестабильной области, наоборот, одинаковые отклонения концентрации от среднего значения сопровождаются большим уменьшением свободной энергии при отклонении в сторону точки перегиба, чем ее возрастание при отклонении в другую сторону, т.е. любые флуктуации концентрации ведут к уменьшению свободной энергии и должны самопроизвольно расти, ограничиваясь только кинетическими (диффузионными) эффектами.

Теоретическое описание механизма и кинетики спинодального распада некристаллизующихся бинарных полимерных смесей базируется на определении свободной энергии смеси состава φ, содержащей малые флуктуации концентрации, с помощью функционала (функции произвольных функций) Гинзбурга-Ландау: 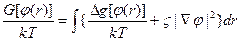, где 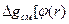] – плотность свободной энергии как функция концентрации и вектора положения r, т.е. размера системы, 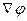- градиент концентрации, ς – константа, учитывающая вклад флуктуаций концентрации и характеризующая естественную шкалу (масштаб) размеров флуктуаций в данной конкретной системе. Для аморфных полимерных бинарных смесей она связана с размерами полимерных клубков: 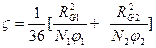, где R_Gi – радиус инерции статистического клубка. При N₁=N₂=N и R_G1=R_G2=R_G=AN^1/2, где А – длина статистического сегмента полимерных цепей:

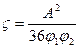. Предполагается, что параметр ς является размерной константой системы, аналогичной временной константе колеблющейся системы типа периода колебаний маятника, не зависящего от амплитуды при малых ее величинах.

В соответствие с классической теорией спинодального распада Кана-Хилларда разность свободной энергии статистически гомогенной смеси и с флуктуациями концентрации ΔG, определенная с помощью функционала Гинзбурга-Ландау и являющаяся термодинамической движущей силой спинодального распада, равна: ,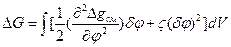

где δφ=φ_i-φ_i,0 – разность локальной и равновесной концентраций i-го компонента соответственно; V – общий объем смеси.

Кинетика роста фаз при спинодальном распаде описывается потоками компонентов, связанными с коэффициентами трансляционной диффузии макромолекул уравнением Фика, в котором градиент концентрации или активности заменен на разность химических потенциалов, рассчитываемых как первая производная свободной энергии по составу. Так, поток компонента 1 в расплаве смеси 1-2 равен: 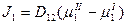, а скорость роста флуктуаций (доменов): 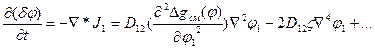, где 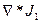- мера пространственного изменения потока из бесконечно малого элемента объема, или мера отклонения от установившегося потока, когда вход и выход одинаковы.

Коэффициент диффузии макромолекул равен: 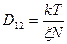при отсутствии зацеплений цепей и 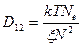- при их наличии, где ξ – коэффициенты трения мономерных звеньев компонентов, N_e – степень полимеризации цепей между зацеплениями; А₀ – длина сегмента Куна, принимаемая равной длине мономерного звена, одинаковая для обоих компонентов.

Решение приведенного выше кинетического уравнения роста фаз при спинодальном распаде дает экспоненциальное выражение для локального градиента концентрации во времени t в точке пространства, определяемой вектором положения r, в виде разложения Фурье с суммированием по всем волновым векторам (волновым числам) β или длинам волн λ, (β=2π/λ) флуктуаций концентрации:

,

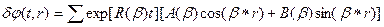где А и В – константы, определяемые Фурье-анализом флуктуаций в исходном состоянии (t=0); R(β) –коэффициент усиления амплитуды флуктуаций концентрации, или линейная скорость роста флуктуаций с волновым числом β:

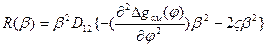
Разложение Фурье позволяет анализировать его составляющие с термодинамических и кинетических точек зрения независимо. Анализ разложения Фурье показывает, что синусоидальные компоненты флуктуаций концентрации возрастают или спадают по амплитуде в зависимости от того, какой знак имеет коэффициент усиления. При 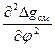>0, т.е. выше спинодали (вне нестабильной области), R(β) отрицателен при любом значении β, и любая существующая флуктуация в эти условиях рассасывается. В нестабильной области, где 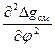<0, R(β) положителен, и все флуктуации самопроизвольно растут с образованием периодической или квазипериодической доменной структуры, периодичность которой определяется длиной волны флуктуаций концентрации. Соответствующее условиям 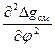=0 и R(β)=0 критическое значение β (β_с) характеризует волновое число, выше которого амплитуда флуктуаций концентрации растут, а ниже – рассасываются. Введение β_с позволяет записать уравнение для R(β) в виде:

.

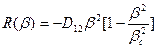Из этого уравнения видно, что максимальной величине R(β) соответствует волновому вектору β_m, равному: 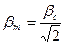, который связан с длиной волны флуктуаций концентрации, характеризующей периодичность образующейся доменной структуры: .

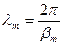На начальной стадии спинодального распада формируется уникальная фазовая морфология, состоящая из статистически распределенных доменов сосуществующих фаз (растущих флуктуаций концентрации) и диффузионной зоны между ними, толщина которой возрастает при приближении к температуре спинодали Т_s и становится бесконечной при Т= Т_s. Параметр периодичности структуры λ_m связан с модулем разности температур |Т- Т_s| соотношением: 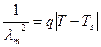, где q – константа (Рис.5). На более глубоких стадиях спинодального распада рост амплитуды флуктуаций концентрации замедляется, и начинает превалировать процессы поглощения мелких доменов более крупными вследствие выигрыша в свободной поверхностной энергии. Эти процессы ничем не отличаются от последней стадии нуклеационного механизма фазового распада. При этом рост объема частиц пропорционален времени: 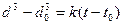, где d и d₀ – средний диаметр частиц во время t и t₀ соответственно, k – константа скорости.. На предельных стадиях фазового разделения аморфные смеси в вязко-текучем состоянии стремятся к расслоению, если предыдущая структура не была кинетически стабилизирована вследствие возрастания диффузионных ограничений, в первую очередь при стекловании одной или обоих фаз.

Рис.5. Изменение фазовой морфологии во время спинодального распада (с.) при фотополимеризации ЭГА, содержащем 80% ЖК

Особое место среди конденсированных полимерных систем занимают блоксополимеры, к которым относится огромное число линейных, разветвленных и сетчатых полимеров, состоящих из двух или нескольких типов достаточно длинных полимерных цепей, химически связанных по концевым звеньям с образованием различной молекулярной топологии (архитектуры). Простейшим случаем являютсялинейные некристаллизующиеся и кристаллизующиеся бинарные диблоксополимеры типа АБ. С термодинамической точки зрения диблоксополимеры являются типичными бинарными полимерными смесями. При этом попарное соединение макромолекул двух типов, как и их смесь без химического связывания, мало влияет на их молекулярное (броуновское) тепловое движение и межмолекулярное взаимодействие (термодинамический параметр χ) и, следовательно, на их равновесное фазовое состояние. Однако, попарное соединение макромолекул двух типов резко изменяет возможности распределения компонентов в условиях фазового разделения.

Схематически расчетная диаграмма состояния диблок сополимера А-В в координатах χN (Т^-1) – n_А и типичные периодические структуры, проявляющиеся в различных ее областях, приведены на Рис. 6-7.

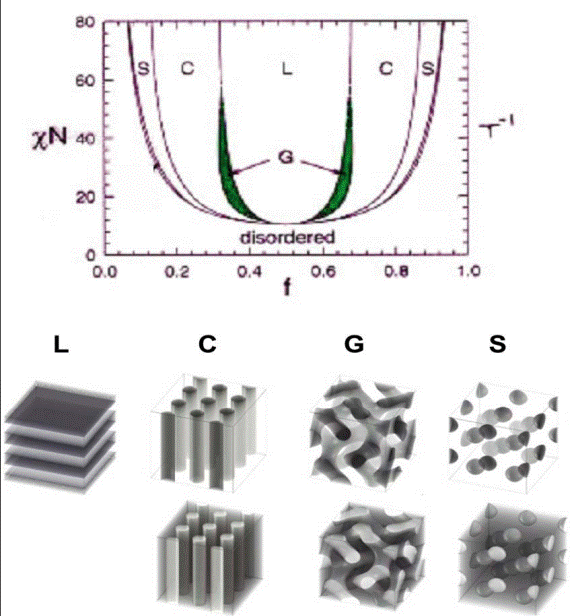
Рис.6. Схемы расчетных диаграмма состояния диблок сополимера А-В в координатах χN (Т^-1) – n_А и типичные периодические структуры, проявляющиеся в различных областях диаграммы

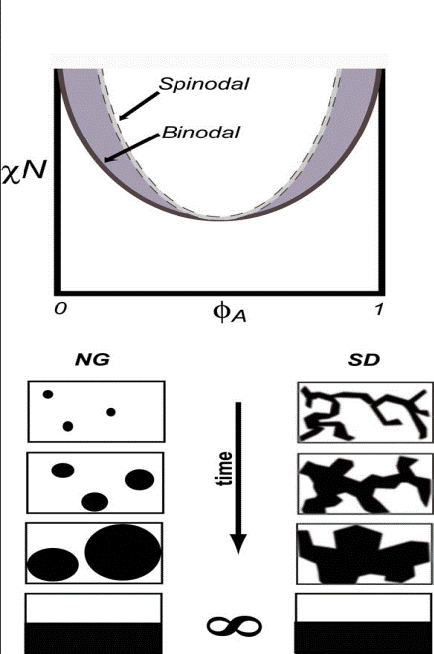
Рис. 7. Схема фазовой диаграммы симметричной смеси гомополимеров и формирования фазовой морфологии при разделении фаз в метастабильной области (зарождение, рост и слияние фаз) NG и в нестабильной области (спинодальный распад) SD

Основным процессом фазового разделения блоксополимеров является не макро-, а микрофазное разделение, или локальное сегрегирование блоков, протекающее по механизму нуклеации или спинодального распада с упорядоченным (периодическим) распределением микрофазных доменов. Положительный вклад энтальпии в свободную энергию в результате уменьшения числа контактов блоков А и В в процессе их локального сегрегирования компенсируется уменьшением энтропии системы в результате локализации узлов соединения блоков на границе раздела фаз и необходимого растяжения цепей от этой границы для обеспечения равномерной плотности их упаковки. Поэтому при повышенной температуре, когда превалирующую роль играет энтропийный фактор, локальное сегрегирование отсутствует. Более низкая температура, при которой энтальпийный фактор становится превалирующим, соответствует температуре упорядоченного микрофазного разделения, или перехода «беспорядок-порядок» c образованием так называемой суперкристаллической (супрамолекулярной) структуры с заданным размером и регулярным расположением структурных элементов (микрофаз в виде тонких пластин, или ламелей, сфер, цилиндров и др.) при неупорядоченной надмолекулярной структурой микрофаз. При этом формирование фазовой морфологии в решающей степени определяется произведением: χN, где N=N_A+N_B (χ_крN=2) и относительной длиной блоков: n_А=N_A/(N_A+N_B:

χN<1 соответствует неупорядоченному состоянию и отсутствию локального сегрегирования блоков;

χN ≈10 соответствует переходу «беспорядок-порядок» и проявлению сегрегирования блоков по механизму спинодального распада со сравнительно слабой движущей силой и формированием периодической микрофазной структуры;

χN >>10 соответствует сегрегированию блоков цепей с формированием периодической структуры с резко выраженной границей раздела между практически индивидуальными А и В доменами с вытянутыми конформациями цепей до R_G~N^2/3.

Одинаковая длина блоков обеспечивает образование ламелярных упорядоченных структур (суперкристаллов), а различная – преимущественно формироваие цилиндрических или сферических микрофаз, состоящих из более коротких блоков (миноргого компоента).

Направленное регулирование морфологии суперкристаллической структуры регулированием длины и природы блоков, а также совмещением блоксополимеров с различной длиной блоков, блоксополимеров с гомополимерами, диблоксополимера А-В с гетерофазной смесью гомополимеров А и В, триблоксопролимера АВС со сравнительно низкомолекулярным диблок сополимером ас и др. (Рис.6).

Рис.6. Схематическая модель (а) и ПЭМ микрофотография (в) взаимопроникающей спиралевидной морфологии диблоксополимера Полистирол/ Полиизобутилен после селективного вытравления УФ/озоном ПИ

В настоящее время для описания динамики формирования структур в непрерывных (исходно гомогенных) средах любого масштаба в условиях, далеких от равновесия, широкое распространение находит обобщенная модель, называемая механизмом Киббла-Зурека (МКЗ). МКЗ описывает превращение гомогенной среды (скалярного поля) с большей симметрией (меньшей упорядоченностью) в среду с меньшей симметрией (с большей упорядоченной) в результате формирования структур (паттернов, ячеек или узоров), состоящих из коррелированных областей (доменов) и топологических дефектов, или фазовых сингулярностей (локальных состояний бифуркации) с еще меньшей симметрией, возникающих по границам коррелированных областей. Топологические дефекты, играющие определяющую роль в превращениях с изменением симметрии, являются результатом ограничений, накладываемых на эволюцию доменов окружающей средой. Физически это означает несогласование по фазе двух (или более) эквивалентных доменов и возникновение топологических дефектов в местах, где отсутствует фазовое согласование. Расстояния между топологическими дефектами дают, в среднем, размер (длину) коррелированных областей.

Киббл использовал такие представления при разработке космологической теории формирования Галактик после Большого взрыва, предположив, что образование топологических дефектов (струн или вихрей) определяет свойства Галактик. Зурек распространил такой подход к описанию динамики критических (непрерывных фазовых) переходов, т.е. фазовых переходов второго рода по определению Эренфеста, в гомогенных конденсированных средах для получения возможности проверки в лабораторных условиях космологических теорий. Применительно к непрерывным фазовым превращениям в конденсированных материальных системах МКЗ предполагает, что определяющий (контрольный) параметр порядка распространяется линейно с заданной лимитирующей скоростью, примерно равной для конденсированных систем скорости звука. При охлаждении до некоторой критической температуры состояние системы изменяется адиабатически и соответствует локальным равновесным состояниям, которые определяются мгновенным значением контрольного параметра. При приближении к критической температуре равновесная корреляционная длина изменяется быстрее, чем лимитирующая скорость и, соответственно, резко изменяется время релаксации вследствие замедления определяющих релаксационные процессы мод (форм) движения. В критической точке (Тс) потенциальный барьер коррелированных областей достигает или превышает энергию теплового движения, процесс формирования узора, т.е. динамика системы, «замораживается», размеры доменов и распределение дефектов стабилизируются, а корреляционная длина достигает предельного значения. Таким образом, критическая температура лимитирует размеры корреляционных областей (доменов) ξ. Она соответствует температуре Гинзбурга (T_G), при которой энергия теплового движения сопоставима со свободной энергией коррелированных областей 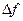: 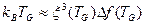(97).

В случаях больших градиентов температуры или высоких скоростей ее изменения при охлаждении, в том числе при переохлаждении метастабильных жидкостей, МКЗ предполагает универсальные степенные соотношения (скейлинг) для зависимостей корреляционной длины параметра порядка (ξ) и времени релаксации (τ) от скорости (характерного времени) охлаждения, причем критические показатели степени (экспоненты) в этих законах зависят только от типа модели (размерности пространства, топологии и характера диссипативных процессов в системе): 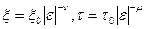(98), где 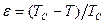, Тс – критическая температура, ν и μ - критические экспоненты. В простейшем случае среднего поля, в предположении, что взаимодействие любой молекулы с окружающими молекулами описывается их средним полем, ν =1/2, μ =1. Характерное время охлаждения τ_q связано c ε, т.е. с удаленностью от Тс, и со скоростью охлаждения (dT/dt) примерными соотношениями: τ_q=t/ε и 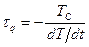(99), где t – текущее время. В момент времени t* система стабилизируется («замораживается») при приближении к температуре Гинзбурга, и в соответствие с МКЗ предельно достигаемый размер коррелированных областей (доменов) зависит только от скорости охлаждения (характерного времени закалки) τ_q в соответствие со скейлинговым соотношением: 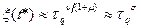(100). В случае среднего поля критическая экспонента σ= 1/4.

В классической равновесной термодинамике проблема стабильности макроскопических материальных систем при постоянном составе, температуре и давлении или объеме в равновесном состоянии, за исключением химического равновесия, сводится к проблеме стабильности однородной (гомогенной) фазы, т.е. каким условиям должна удовлетворять гомогенная система, чтобы она не стала гетерогенной (не распалась на две отличные от первоначальной макроскопической) фазы в результате внешних или внутренних (локальных, микроскопических) возмущений (флуктуаций). Наиболее общий критерий стабильности такой фазы предложил Гиббс: если энергетическое выражение фундаментального термодинамического уравнения в интегральной форме 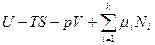при определенных значениях интенсивных параметров Т, р, 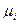для какой-либо фазы равно нулю, а для любой другой фазы, образованной из тех же компонентов, при тех же условиях будет больше нуля, то рассматриваемая фаза по отношению к распаду на другие фазы является абсолютно стабильной.

На основе этого критерия и в соответствие с принципом Ле Шателье (если на систему, находящуюся в равновесии, оказывать какое-либо воздействие, отклоняющее от равновесия, то в системе будут протекать процессы, уменьшающее это воздействие) Гиббсом и Дюгемом была разработана классическая термодинамическая (энергетическая) теория устойчивости равновесных состояний к случайным локальным возмущениям (флуктуациям) термодинамических параметров состояния - независимых переменных: температуры (δТ), объема (δV), состава (δN_k) или давления (δр), т.е. случайными отклонениями этих величин от значений, соответствующих нормальному, наиболее вероятному (максвелловскому) распределению частиц, образующих систему, по энергиям, т.е. от их средних равновесных (наиболее вероятных) значений. При энергетическом подходе в термодинамике теория устойчивости равновесных состояний к флуктуациям термодинамических параметров базируется на постулате о возрастании термодинамического потенциала (свободной энергии) при возникновении флуктуаций относительно его минимального значения. Соответственно, в системе возникают самопроизвольные (спонтанные) необратимые процессы, ослабляющие этот эффект (принцип Ле Шателье), т.е. уменьшающие свободную энергию за счет положительного приращения энтропии (Δ_iF=ΔU-TΔ_iS <0 или Δ_iG=ΔH-TΔ_iS <0 ), сохраняя систему в равновесном состоянии. Таким образом, условием стабильности равновесного состояния является то, что возникновение флуктуаций, являясь энергетически невыгодным процессом, сопровождается увеличением термодинамических потенциалов (Δ_фF >0 и Δ_фG >0), что вызывает самопроизвольное возникновение необратимых процессов, уменьшающих эти потенциалы. Если возникновение и рост флуктуаций станет энергетически выгодным (Δ_фF <0 и Δ_фG <0), то флуктуации должны самопроизвольно расти, система становится неустойчивой и должна перейти в новое состояние.

Для оценки изменения термодинамического потенциала (в общем случае Ψ) вследствие возникновения флуктуаций термодинамических параметров (Δ_фΨ) оно разлагается в степенной ряд Тейлора по вариациям изменения: Δ_фΨ=δΨ+ 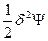+ … (71), в котором член первого порядка малости δΨ является функцией первой степени флуктуаций температуры (δТ), объема (δV), состава (δN_k), а член второго порядка малости 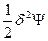- функцией второй степени этих флуктуаций, т.е. (δТ)², (δV)² и (δN_k)² и т.д. Основной вклад в изменение термодинамических потенциалов вследствие возникновения флуктуаций вносят члены второго порядка малости, поэтому условием устойчивости равновесного состояния является положительное значение этого члена ряда 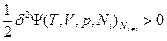или, соответственно, для свободных энергий Гельмгольца: 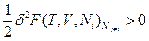и Гиббса:.

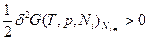При использовании энтропийной формы фундаментального уравнения применительно к изолированным системам предполагается, что флуктуации термодинамических параметров уменьшают энтропию относительно ее максимального значения (Δ_фS <0). Возникающие в системе самопроизвольные (спонтанные) необратимые процессы ослабляют это воздействие в соответствие с принципом Ле Шателье, т.е. увеличивают энтропию за счет ее положительного приращения (Δ_iS >0) до максимального значения, сохраняя равновесное состояние. Поэтому условием стабильности равновесного состояния изолированных систем является термодинамичнеская невыгодность возникновения и роста флуктуаций, т.е. уменьшение вследствие этих процессов энтропии (Δ_фS <0). Если возникновение и рост флуктуаций является или становится термодинамически выгодным (Δ_фS >0), то они должны самопроизвольно расти, и система теряет устойчивость к ним.

Уменьшение энтропии, вызываемое флуктуациями термодинамических параметров, также как увеличение термодинамических потенциалов при этом, разлагается в степенной ряд Тейлора по вариациям: Δ_фS=δS+ 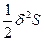+ … (72), причем членами ряда более высокого порядка малости, чем 2, обычно пренебрегают. В данном разложении член первого порядка малости δS является функцией первой степени флуктуаций температуры (δТ), объема (δV) или состава (δN_k), а член второго порядка малости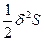- функцией второй степени этих флуктуаций, т.е. (δТ)², (δV)² и (δN_k)², причем δS =0, и основной вклад в изменение энтропии вследствие возникновения флуктуаций вносит второй член разложения, т.е. 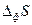=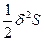. При этом условием устойчивости системы к флуктуациям термодинамических параметров является отрицательное значение этого члена ряда: 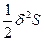<0.

Термодинамические расчеты вариаций энтропии вследствие флуктуаций температуры, объема и состава (числа молей компонентов) в изолированной системе в равновесном состоянии были проведены Гиббсом и Дюгемом в предположении, что флуктуация происходит в малой (локальной) части (обозначается индексом 1) макроскопической системы, основная часть которой обозначается индексом 2, и не нарушает общее состояние системы:

• Локальная флуктуация внутренней энергии заключается в ее изменениях для частей системы 1 и 2 при сохранении неизменной общей энергии системы (δU₁=-δU₂=δU). При этом значения первой и второй вариации энтропии равны: 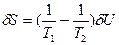(73) и 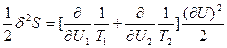(74). В равновесии термодинамические силы и потоки отсутствуют, и температура в обеих частях системы одинакова, т.е. Т₁=Т₂. Следовательно, первая вариация энтропии δS=0. В формуле для второй вариации 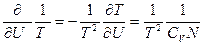(75), где 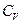- мольная теплоемкость. Подставляя уравнение (75) в (74), получаем: 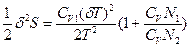(76), где δТ - изменение температуры (тепловая флуктуация) в малой части системы. Так как часть 1 системы мала по сравнению с основной частью 2 ( 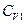N₁ <<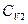 N₂), то 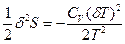(77). Таким образом, условием устойчивости системы к тепловым флуктуациям(тепловой устойчивости) и равновесного состояния является Δ_фS= 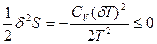, причем эти условия соблюдаются только при положительном значении теплоемкости системы, т.е.при 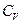>0.
• Локальная флуктуация объема заключается в изменениях объема частей системы 1 и 2 при сохранении неизменным общего объема, т.е. δV₁=-δV₂=δV. Аналогично предыдущему cлучаю значения первой и второй вариации энтропии равны: 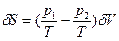(78) и 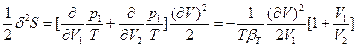<0 (79), где 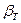- изотермическая объемная сжимаемость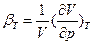. Так как в равновесии 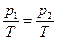, то δS =0, а так как V₁ << V₂, то 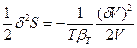(80). Таким образом, условием устойчивости системы к флуктуациям объема или плотности (механической устойчивости) и равновесного состояния является 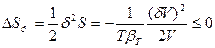, причем эти условия обеспечиваются только при положительном значении объемной сжимаемости (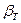>0).
• Локальная флуктуация числа молей компонентов в многокомпонентной системе, обусловленная диффузионным обменом молекулами межу частями 1 и 2 (δN_k1=-δN_k2=δN_k) при сохранении неизменным их общего количества, определяет следующим образом значения первой и второй вариации энтропии: 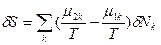(81) и 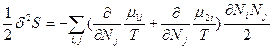(82). В равновесном состоянии 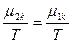, следовательно δS =0, а так как часть системы 1 намного меньше части 2, то 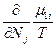>>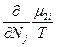и 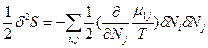(83). Таким образом, условием устойчивости системы к флуктуациям концентрации и равновесного состояния является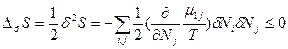, причем эти условия обеспечиваются только при положительном значении химического потенциала (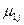>0). Эти условия могут быть также применено к устойчивости химического равновесия к флуктуациям степени превращения δξ в химических реакциях в предположении, что δN_k =υ_kδξ, где υ_k – стехиометрический коэффициент. 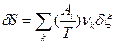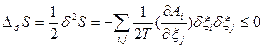Тогда и (84).

Таким образом, при флуктуациях основных термодинамических независимых переменных (δТ, δV и δN_k) общее изменение энтропии при возникновении флуктуаций температуры, плотности и концентрации или химического превращения и условие устойчивости к ним равновесного состояния может быть выражено обобщенным уравнением: 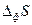= 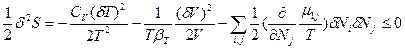<0 (85). В этом выражени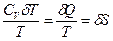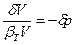и , и 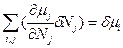. Тогда уравнение (85) можно записать через произведение парных переменных: 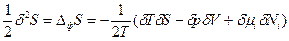(86).

Обобщенная термодинамическая теория флуктуаций, развитая Эйнштейном, позволяет рассчитывать по величине 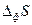вероятности флуктуаций термодинамических параметров в равновесном состоянии. Как хорошо известно, впервые идею вероятности в термодинамику ввел Больцман, который предположил, что энтропия любой макроскопической системы равна: 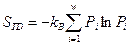(87), где 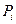- вероятность 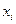состояния в множестве дискретных состояний при i =1,2, …, w. При равновероятном состоянии всех 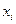состояний, т.е при Р₁=Р₂=….=Р_i= 1/ w выражение (87) дает известное соотношение Больцмана: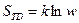, где w – число микросостояний, соответствующих макросостоянию системы, энтропия которой равна 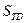. Это число по предложению Макса Планка иногда называют термодинамической вероятностью, которая, в отличие от обычной вероятности, значительно больше единицы.

Эйнштейн, в противоположность Больцману, применившему термодинамическую вероятность для вывода энтропии, наоборот, использовал энтропию для вывода вероятности термодинамических флуктуаций: 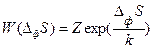(88), где Z – нормировочный множитель, обеспечивающий равенство суммы всех вероятностей 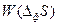единице, а 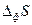- изменение энтропии вследствие возникновения флуктуации независимых термодинамических параметров. Подстановка в формулу Эйнштейна (88) значения 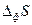в соответствие с уравнением (85) дает общее выражение для вероятности флуктуаций δТ, δV и δN_k: 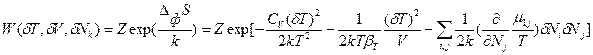(89). В более простом виде с учетом соотношения (86) это выражение может быть записано через произведение парных переменных:

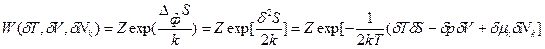(90).

Нормировочный множитель определяется как 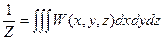, а распределение вероятности принимается гауссовым для каждой независимой переменной δТ, δV и δN_k. Использование этих представлений и приведенных соотношений позволяет определить вероятность флуктуаций в явном виде и рассчитать их среднеквадратичные значения.

При обобщенной записи уравнения (90) для любого набора независимых термодинамических параметров Х_k, флуктуации которых от равновесного значения обозначаются как δ Х_k, и заменяют переменные δТ, δV и δN_k, изменение энтропии за счет этой флуктуации есть квадратичная функция δ Х_k: 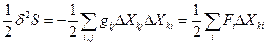(90), где 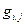- коэффициент пропорциональности, а 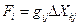- термодинамическая сила. Например, для изменения энтропии, вызванного флуктуациями степени превращения в r химических реакциях (см. уравнение 84) 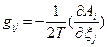, а 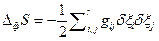. При наличии распределения вероятности для набора переменных δ Х_k эти соотношения позволяют определять средние значения любой функции этих переменных и корреляции между парами переменных. Установлено, что каждая флуктуация коррелирует только с соответствующей и ни с какой другой термодинамической силой. Среднее значение флуктуаций энтропии для m независимых переменных δ Х_k равна: 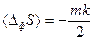, где k –константа Больцмана, т.е. каждый независимый процесс вносит вклад в изменение энтропии, обусловленное флуктуациями термодинамических параметров, равный –k/2, причем знак минус показывает, что флуктуации уменьшают энтропию. Этот результат аналогичен теореме статистической механики, согласно которой каждая степень свободы теплового движения дает вклад в увеличение средней энергии, равный kТ/2. С помощью этих соотношений получен простой вывод соотношений взаимности Онсагера.