В качестве одномерной модели твердого тела рассмотрим цепочку из n одинаковых атомов с массой М и межатомным расстоянием а, которые могут перемещаться вдоль прямой линии (рисунок 7.3).
 |
Каждый атом в такой системе обладает одной степенью свободы, а вся система – N степенями свободы.
Допустим, что в момент времени t = 0 мы сместили из положения равновесия атом с номером n = 0 на расстояние u0. Так как атомы в цепочке связаны друг с другом силами связи, то такое возбуждение распространится по цепочке в виде волны сжатия, и все остальные атомы сместятся из своих положений равновесия.
Пусть un(x, t) – это смещение в какой-то момент времени n -го атома относительно его положения равновесия в точке с координатой xn=n∙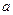 . Если смещения атомов из положения равновесия малы по сравнению с расстоянием
. Если смещения атомов из положения равновесия малы по сравнению с расстоянием 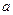 , то силы межатомного взаимодействия можно считать квазиупругими (согласно закону Гука, они пропорциональны смещениям). Атомы в цепочке как бы связаны между собой упругими пружинками, каждая из которых характеризуется упругой постоянной С, а смещение un описывает колебания атома вблизи положения равновесия.
, то силы межатомного взаимодействия можно считать квазиупругими (согласно закону Гука, они пропорциональны смещениям). Атомы в цепочке как бы связаны между собой упругими пружинками, каждая из которых характеризуется упругой постоянной С, а смещение un описывает колебания атома вблизи положения равновесия.
Найдем уравнение движения n -го атома. Будем считать, что каждый атом взаимодействует лишь с ближайшими соседями, которые оказывают на него наиболее сильное влияние. Влиянием более удаленных атомов будем пренебрегать. Рассмотрим силы, действующие на n -й атом. Исходя из предположения о взаимодействии с ближайшими соседями, силы, действующие на n -й атом, можно представить в виде результирующей силы:
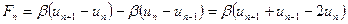 ,
,
где b – силовая постоянная, которая связана с упругой постоянной С = b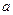 .
.
Зная выражение для силы, запишем закон движения n -го атома:
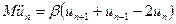 .
.
Решение этого уравнения будем искать в виде бегущей волны:
un=u0exp[i(k∙n∙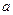 -w∙t)]= u0∙exp[i(k∙хn-w∙t)],
-w∙t)]= u0∙exp[i(k∙хn-w∙t)],
где u0 – определяет смещение атома с n = 0 в момент времени t = 0;
w – круговая частота;
k = 2p/l – волновое число.
Подставим решение в уравнение движения n -го атома:
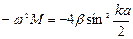 .
.
Из данного выражения следует дисперсионное соотношение для волн, распространяющихся в цепочке из одинаковых атомов:
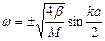 .
.
Поскольку w не может быть отрицательной величиной, минус соответствует области отрицательных значений k (рисунок 7.4).
Из анализа закона дисперсии следует, что при значении волнового числа 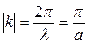 , т. е. при коротких длинах волн l = 2а, циклическая частота колебаний достигает максимального значения w = wmax =
, т. е. при коротких длинах волн l = 2а, циклическая частота колебаний достигает максимального значения w = wmax = 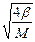 .
.
 |
Оценим величину wmax»
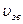 k, где
k, где 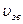 – скорость распространения акустических волн. Можно считать, что
– скорость распространения акустических волн. Можно считать, что 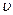 = 5×103 м/с. Если принять для твердых тел
= 5×103 м/с. Если принять для твердых тел 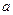 = 3×10-10 м, то
= 3×10-10 м, то 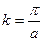 » 10-10 м-1 и wmax» 5×1013с-1, что по порядку величины соответствует частотам тепловых колебаний атомов в твердых телах.
» 10-10 м-1 и wmax» 5×1013с-1, что по порядку величины соответствует частотам тепловых колебаний атомов в твердых телах. При малых значениях k (что соответсвует длинам волн, значительно большим, чем расстояния между атомами в цепочке) w зависит от k линейно, как и для случая непрерывной упругой струны с линейной плотностью.
Таким образом, отличие дискретной цепочки от непрерывной струны заключается в отсутствии пропорциональности между частотой w и волновым числом k. Это связано с дисперсией волн. Короткие волны, которым соответствует более высокая частота колебаний частиц, вследствие инерции масс частиц распространяются медленнее, чем длинные волны. Наличие дисперсии волн проявляется в отклонении кривой w = w(k) от линейной зависимости, справедливой для упругой струны. Цепочка из одинаковых атомов ведет себя в отношении распространения акустических волн как упругая струна только лишь при длинах волн l >> 2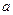 .
.
 2014-02-09
2014-02-09 1620
1620








