Системы счисления. Преобразование переключательных функций в различных базисах

Преобразование переключательных функций в различных базисах

Раздел 1. Переключательные функции и их минимизация

Преобразование переключательных функций в различных базисах

Содержание

ТИПОВЫЕ ЭЛЕМЕНТЫ И УСТРОЙСТВА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

Формирование, распределение и использование прибыли в торговле.

В процессе производственно-финансового плана результатов работы торговой организации применяются различные показатели прибыли: прибыль (убыток) от реализации товаров; прибыль от реализации основных фондов и иного имущества; валовая (балансовая) прибыль; чистая прибыль (прибыль, остающаяся в распоряжении предприятия). Различия понятий прибыли определяются их экономическим содержанием и положениями законодательства о налогообложении прибыли организации.

Прибыль (убыток) от реализации товаров определяется как разность ме6жду валовым доходом от реализации товаров (без учета налога на добавленную стоимость) и издержками обращения.

Взаимоотношения с бюджетом и распределение прибыли аналогичны тем, что существуют в промышленности.

Раздел 1. Переключательные функции и их минимизация

1.1. СИСТЕМЫ СЧИСЛЕНИЯ

1.2. ЛОГИЧЕСКИЕ КОНСТАНТЫ И ПЕРЕМЕННЫЕ. ОПЕРАЦИИ БУЛЕВОЙ АЛГЕБРЫ

1.3. СПОСОБЫ ЗАДАНИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ

Словесное описание ФАЛ

Описание ФАЛ в виде таблицы истинности

Описание ФАЛ в виде алгебраического выражения

Описание ФАЛ в виде последовательности десятичных чисел

Ошибка! Источник ссылки не найден.

1.4. ОСНОВНЫЕ ТЕОРЕМЫ И АКСИОМЫ АЛГЕБРЫ ЛОГИКИ (БУЛЕВОЙ АЛГЕБРЫ)

Основные аксиомы алгебры-логики

Другие соотношения

Следствия

Существующие системы счисления подразделяются на позиционные и непозиционные. В непозиционных системах значение конкретной цифры постоянно и не зависит от ее расположения в записи числа. Примером такой системы счисления является Римская система записи числа. Например, в числе XXXVII значение цифры Х не зависит от ее местоположения в записи числа. Оно везде равно 10.

В позиционных системах счисления значимость конкретной цифры определяется ее местоположением в записи числа. Так, произвольное число Х в позиционной системе счисления с основанием q в общем случае можно представить в виде полинома

Х_q = х_п-1 q ^п-1 + х_п-2 q ^п-2 + … + х₀ q ⁰ + х_-1 q^-1 + … + х_-m q ^-m (1.1)

где х_i — разрядный коэффициент (х_i = 0... q — 1); qⁱ — весовой коэффициент.

Число q называется основанием системы счисления. Следует отметить, что число q может быть как целым, так и дробным.

Если в выражении (1) отбросить весовые коэффициенты q ' и соответствующие знаки сложения, то получим сокращенную запись числа, носящую название q -ичного кода числа Хq. Номер позиции цифры х_i называют его разрядом. Разряды с положительными степенями q образуют целую часть числа Х q, с отрицательными степенями — дробную. Цифры х_п-1 и х_-m соответственно являются старшим и младшим разрядами числа.

Количество различных чисел, которое может быть записано в позиционной системе счисления с основанием q при заданном числе разрядов,

N = q ^{п + m} (1.2)

Количество разрядов, необходимое для записи в позиционной системе счисления с основанием q некоторого числа Х, можно определить из следующих соображений. Согласно (2), для записи числа Х в системе с основанием q должно выполняться условие Х_q £ q ^{п + m} — 1. Тогда

n + т ³ 1оg_q (Х_q + 1) (1.3)

В цифровой технике нашли применение только позиционные системы счисления.

Для представления числа, записанного и позиционной системе счисления с выбранным основанием q, при помощи электрических сигналов необходимо иметь некоторое электронное устройство, формирующее на выходе q различных электрических сигналов,. которые достаточно легко можно отличить друг от друга. При этом необходимое число таких устройств должно равняться числу разрядов целой и дробной частей записываемого числа.

Очевидно, что в этом случае чем больше величина q, тем меньше понадобится указанных электронных устройств. С другой стороны, увеличение q потребует создания сложных электронных блоков, способных формировать на выходе большое число различных электрических сигналов. В этом случае, например при использовании в качестве информационного параметра уровня напряжения при фиксированной его максимальной величине, с увеличением q уменьшается различие между дискретными уровнями выходных сигналов, что в конечном счете усложняет их идентификацию. Последнее повышает вероятность появления ошибок при действии внешних помех и усложняет само устройство.

Критерием выбора q в данном случае является минимизация аппаратных затрат при обеспечении достаточной помехоустойчивости. Попытки чисто математического решения поставленной задачи показали, что оптимальной при поставленных требованиях является система счисления с основанием е = 2,71.... Однако практически создать такую систему сложно и технически нецелесообразно.

Широкое распространение в цифровой технике получила позиционная система счисления с основанием q = 2 — двоичная система счисления. По определению в такой системе фигурируют только два цифровых знака 0 и 1.

При работе с устройствами вычислительной техники приходится сталкиваться с позиционными системами счисления с основанием 2, 8, 10 и 46. Рассмотрим ряд правил, позволяющих выполнить преобразование чисел из одной системы счисления в другую.

Переход от системы счисления с меньшим основанием к системе счисления с большим основанием осуществляется при помощи выражения (1), которое справедливо как для целой, так и для дробной частей числа.

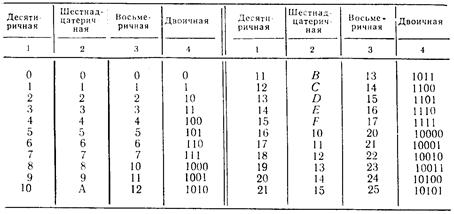
Таблица 1

Натуральный ряд чисел в различных системах счисления

Пример 1.1. Преобразовать двоичное число Х₂ = 1011₂ в десятичное Х₁₀

Р е ш е н и е. Согласно выражению (1.1) для q = 2 получим Xio = l ^. 2³ +. l ^. 2² + l ^. 2¹ +

+ l ^. 2⁰ = 11

Переход от системы счисления с большим основанием к системе счисления с меньшим основанием выполняется с соблюдением следующих правил:

а) целая часть исходного числа делится на основание новой системы счисления;

б) дробная часть исходного числа умножается. на основание новой системы счисления.

Пример 1.2. Преобразовать в двоичную систему счисления десятичное число 25,12.

Решение. 1. Преобразуем целую часть:

25: 2 = 12 +1 (Хо = 1)

12: 2 = 6 + 0 (Х₁ = 0)

6: 2 = 3 + 0 (Х₂ = 0)

3: 2 = 1 + 1 (Хз = 1)

1: 2 = 0 + 1 (Х₄ = 1)

Запись целой части двоичного числа Х₂ производится с последнего результата деления, т. е. 25₁₀ = 11001₂. 2. Преобразуем дробную часть:

0,12 × 2 = 0 + 0,24 (Х_-1 = 0)

0,24 × 2 = 0 + 0,48 (Х_-2 = 0)

0,48 × 2 = 0 + 0,96 (Х_-3 = 0)

0,96 × 2 = 1 + 0,92 (Х_-4 = 1)

0,92 × 2 = 1 + 0,84 (Х_-5 = 1)

Запись дробной части двоичного числа производится с первого результата умножения, т, е.

0,12₁₀ = 0,0001₂.

3. Окончательно получим: 25,12₁₀» 11001,0001₂.

В табл. 1.1 для примера приведен натуральный ряд чисел в различных системах счисления.

Переход из двоичной системы счисления в восьмеричную или шестнадцатеричную может быть выполнен более простым путем.

Так как 8 = 2³, а 16 = 2⁴, то один разряд числа, записанного в восьмеричной системе счисления, преобразуется в три разряда, а один разряд числа в шестнадцатеричной системе — в четыре разряда числа двоичной системы счисления и наоборот.

Пример 1.3. Преобразовать Х₂ = 1010012 в Х₈.

Решение. Согласно табл.1.1 101₂ = 5₈ и 001₂ = 1₈ , поэтому Х₈ = 51₈.

Пример 1.4. Преобразовать Х₂ = 10100110₂ в Х₁₆.

Р е ш е н и е. Согласно табл. 1.1 1010₂ = А₁₆ и 0110₂ = 6₁₆ , поэтому Х₁₆ = А6₁₆.