Два подхода в определении предела функции.
Критерий Коши существования предела функции.
Свойства пределов функций.
Бесконечно большие и бесконечно малые функции.
Два подхода в определении предела функции.
Понятие функции. Виды функций. Основные элементарные функции.
МА-Лк3
Задание на самоподготовку
Задание для самостоятельной работы
Изучить:
1. Скребов В.Н., Трубилко А.И. Курс общей физики. Т. 2. Электричество и магнетизм. — СПб: СПбУ ГПС МЧС России, 2011, с.126-175
2. Трофимова Т.И. Курс физики. — М.: Высшая школа, 2003. с 180-203
1. Подготовиться к лабораторно-практическим занятиям 7.2,7.3.
Разработал
Доцент А.А. Чумаченко
Тема 3. Функции и их пределы.
3.1.Понятие функции. Виды функций. Основные элементарные функции. (Содержание этого пункта подробно рассмотрено на лекции)
1#. Пусть функция 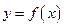 определена на интервале
определена на интервале 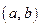 , кроме, быть может, точки
, кроме, быть может, точки 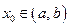 . Число
. Число 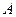 называется пределом функции
называется пределом функции 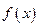 при
при 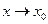 , если
, если 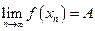 для любой последовательности
для любой последовательности 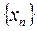 , такой, что
, такой, что
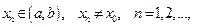 и
и 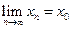 . Если такое число
. Если такое число 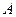 существует, то говорят, что функция
существует, то говорят, что функция 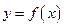 имеет предел в точке
имеет предел в точке 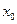 .
.
! Обозначим: 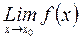 =
= 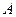 или
или
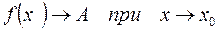 .
.
! Отметим, что определение позволяет утверждать, что функция не может иметь двух разных пределов в одной точке.
! Отметим, что из определения следует: значения функции 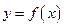 в точках
в точках 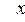 , лежащих в любой фиксированной окрестности точки
, лежащих в любой фиксированной окрестности точки 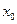 , и значение функции в точке
, и значение функции в точке 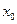 не влияют ни на существование, ни на величину предела функции в точке
не влияют ни на существование, ни на величину предела функции в точке 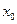 .
.
 : Определите существование предела функции при
: Определите существование предела функции при 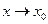 на основе определения предела функции по Гейне:
на основе определения предела функции по Гейне:
а) 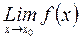 =
= 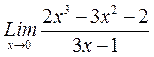 =…
=…
б) 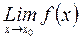 =
= 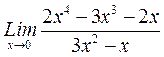 =…
=…
 2014-02-09
2014-02-09 492
492






