Способы описания алгоритмов
Известны несколько способов описания алгоритмов:
1. Словесный. Он наиболее понятен человеку. Его недостатки:
Он не понятен ЭВМ.
Его трудно автоматически превратить в машинную программу.
Иногда неоднозначен (в языке человека есть слова, имеющие смысл, зависящий от контекста).
2. Программный. Это наиболее компактное и пригодное для автоматического создания программы для ЭВМ представление.
3. Графический. Применяется для визуализации логики иерархически организованных программ. Его недостатки:
Громоздкость для больших программ.
Трудоемкость.
Пользователь должен понимать используемые графические символы.
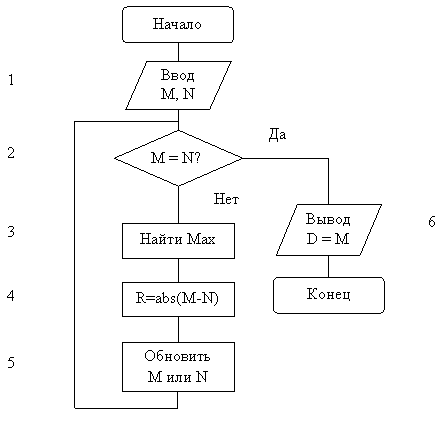
Блоки нумеруются для ссылок на них. Номера размещаются вблизи блока произвольно.
Начало и Конец не нумеруются. Возможны текстовые комментарии
Задача
Найти наибольший общий делитель D двух натуральных чисел M и N.
Натуральное число – целое и положительное
Алгоритм:
1. Ввод M и N.
2. Если M и N одинаковы, то к 6.
3. Определить максимальное Max. Это или M, или N.
4. Найти разность R = abs(M-N).
5. Вставить R на место максимального из M и N. Перейти к пункту 2.
6. Вывести результат D = M.
| M | N | R | № | Комментарий |
| Блок 1 | ||||
| - | 1-1 | M=75, N=45 | ||
| - | 2-1 | Не равны | ||
| - | 3-1 | Max=M=75 | ||
| 4-1 | R=75-45=30 | |||
| 5-1 | M=R=30 | |||
| Перейти к блоку 2 | ||||
| 2-2 | Не равны | |||
| 3-2 | N=Max=45 | |||
| 4-2 | R=45-30=15 | |||
| 5-2 | N=R=15 | |||
| Перейти к блоку 2 | ||||
| 2-3 | Не равны | |||
| 3-3 | Max=M=30 | |||
| 4-3 | R=30-15=15 | |||
| 5-3 | M=R=15 | |||
| Перейти к блоку 2 | ||||
| 2-4 | Равны | |||
| Перейти к блоку 6 | ||||
| 6-1 | D=15 |
 2014-02-09
2014-02-09 331
331







