Лекция 10. Підсумовування похибок ЗВТ

Задача определения расчетным путем значения результирующей погре­шности по известным значениям ряда ее составляющих, называется обычно задачей суммирования погрешности.

В измерительной практике с суммированием погрешностей при­ходится встречаться в следующих случаях:

· при определении погрешностей косвенных, совокупных и со­вместных измерений;

· при определении результирующей погрешности измерительных приборов по погрешностям их звеньев.

Оп­ределение погрешности прибора или канала информационно-измери­тельной системы (ИИС) также сводится к определению суммарного действия погрешностей всех его преобразователей. Таким образом, задача суммиро­вания погрешностей — это одна из основных задач как при проектировании средств измерений, так и при постановке и проведении измерений.

Возможны следующие подходы к решению задачи суммирования погреш­ностей.

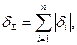Арифметическое суммирование. До недавнего времени иногда резуль­тирующую погрешность и при на­личии случайных составляющих определяли арифметическим суммировани­ем, т. е. находили максимально возможное зна­чение результирующей по­грешности в виде суммы

где | d _i|-абсолютное значение составляющей суммарной погрешности. Полученная таким образом оценка значительно превышала вероятную практическую погрешность, то есть она была «с большим запасом».

Геометрическое суммирование.

Этот метод описан ниже.

Трудность суммирования погрешностей заключается в том, что все составляющие погрешности в общем случае должны рассматри­ваться как случайные величины, принимающие в каждой частной реа­лизации самые разнообразные значения. С точки зрения теории ве­роятностей они могут быть описаны своими законами распределения, а их совместное действие — соответствующим многомерным законом распределения. В такой постановке эта задача становится практически неразрешимой уже для 3—4 составляю­щих.

При этом необходимо учитывать следующее: а ) числовые характерис­тики законов распределения составляющих (например, s и k) могут не оставаться постоянными при изменении измеряемой величины, т. е. могут изменяться в диапазоне ее изменения; б ) отдельные составляющие погреш­ности могут быть коррелированны между собой и в ) при суммировании случайных величин законы их распределения резко деформируются.

Первое из этих обстоятельств требует разделения рассматривае­мых составляющих на аддитивные и мультипликативные, суммирова­ние которых производится раздельно для определения соответственно аддитивной и мультипликативной составляющих результирующей по­грешности.

Второе обстоятельство, т. е. возможность взаимных корреляцион­ных связей составляющих, учитывается путем использования для характерис­тики суммируемых составляющих погрешности их числовых оценок в виде среднего квадратического значения и коэффициентов взаимной корреляции.

Третье обстоятельство, т. е. деформация формы законов распреде­ления при суммировании случайных величин, не может быть учтено при использовании оценки погрешности в виде ее среднего квадратического значения, так как эта оценка не отражает деформации формы законов распределения.

Дисперсия суммы коррелированных и некоррелированных величин. Согласно теории вероятностей дисперсия суммы двух величин в об­щем случае

D(x+y)=D (x) +D (y) + 2 k_xy,

где D (х) — дисперсия х; D (у) — дисперсия у; k_xy = rs (х) s (у) — их вза­имный корреляционный момент. Отсюда среднее квадратическое значение s _S отклонения суммы этих величин от ее математиче­ского ожидания

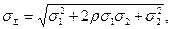
где r — коэффициент корреляции.

В случае n составляющих последняя формула приобретает вид:

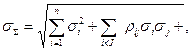
где i < j обозначает, что суммируются все возможные попарные сочетания средних квадратических отклонений коррелированных по­грешностей.

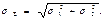Если случайные погрешности некоррелированы между собой, то r=0 и

Однако если х и у жестко и положительно (r = +1) коррелированы между собой, т. е. Dу принимает значения, лишь строго пропорцио­наль­ные Dх, то всякое положительное отклонение +D х сопровождается также положительным отклонением +D у и отклонение D(х + у)складывается как Dх+Dу. Это формально следует и из формулы для s _S при r =+1, ибо

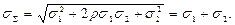
Если же при возрастании х значения у, наоборот, линейно убывают, то r=—1 и

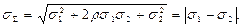
Таким образом, оценки жестко коррелированных погрешностей (r=±1) должны суммироваться не геометрически, а алгебраически с учетом их знаков, т. е. Складыва­ться, когда их знаки совпадают, и вычитаться, когда их знаки оказы­ваются противоположными. Эти поло­жения иллюстрируются рисунком 10.1.

Коэффициент взаимной корреляции r может принимать значения от –1 до +1.

На рис.10.1 вектор ОА соответствует s ₁, а АВ — s ₂. Дуга BE является геометрическим местом точек конца вектора результирующей погрешности при 0< r <1, a BF — при —1< r <0.