Классификация переменных
Примеры известных моделей
Модель «затраты-выпуск» (Модель Леонтьева)
AX + Y = X (1.1)
ЗдесьХ и Y переменные модели, а матрица А параметр модели.
Модель Кобба-Дугласа (производственная функция)
Y = a0•Kα•L(1-α) (1.2)
Здесь (a0,α)-параметры модели, (Y, K, L)- переменные модели.
Замечание. Модель (1.1) представляет собой систему линейных алгебраических уравнений, модель (1.2) состоит из одного (изолированного) уравнения.
Определение. Эндогенной (зависимой) переменной называется такая переменная, значение которой формируется внутри модели в результате взаимодействия с другими переменными.
Определение. Экзогенной (независимой) переменной называется переменная, значение которой формируется вне модели.
Второй принцип спецификации модели состоит в том, что количество уравнений в модели должно равняться количеству эндогенных переменных.
Этот принцип используется, в частности, для контроля за правильностью записи спецификации модели.
Определение. Модели, в состав которых входят только эндогенные переменные, называются замкнутыми.
|
|
|
Если в модели присутствует хотя бы одна экзогенная переменная, модель называется открытой.
Так модели (1.1) и (1.2) являются открытыми, так как в них присутствуют экзогенные (независимые) переменные: конечный спрос ‘Y’ в модели (1.1), труд «L» и капитал «К» в модели (1.2).
Определение. Уравнение модели имеет структурную форму, если оно содержит более одной эндогенной переменной.
Определение. Уравнение модели имеет приведенную форму, если оно содержит только одну эндогенную переменную.
Форма модели в виде системы нескольких уравнений считается структурной, если хотя бы одно из уравнений представлено в структурном виде.
На этапе спецификации модели из нескольких уравнений, как правило, имеют структурную форму.
Модели в виде изолированного уравнения всегда имеют приведенную форму.
3. Модель парной линейной регрессии. Инструментом для создания регрессионных моделей является корреляционно-регрессионный анализ случайных величин.
Существуют различные виды зависимостей 2-х величин друг от друга.
Первая из них – функциональная зависимость, когда определенному значению одной из величин х ставится в соответствие единственное значение другой величины у, т.е. у = f(x).
В экономических и социальных процессах функциональная зависимость встречается редко.
Здесь, как правило, зависимость между двумя величинами является стохастической – неоднозначной и зависящей от случайных воздействий.
При этом различают регрессионную и корреляционную зависимости и соответствующие им модели.
|
|
|
В случае регрессионной зависимости предполагается, что одна из величин (х) является неслучайной и независимой от другой (у). Тогда каждому значению х соответствует совокупность случайных значений у, подчиняющихся некоторому закону распределения с определенным математическим ожиданием и дисперсией.
Регрессионная модель отражает зависимость среднего значения у от фактора х.
Корреляционная модель предполагает, что обе величины являются выборкой из двумерного распределения. В этом случае существуют две линии регрессии – линия зависимости среднего значения у от х и линия зависимости среднего значения х от у.
На практике для описания экономических процессов чаще используют регрессионную модель.
Разработка модели состоит из нескольких этапов.
Первый этап – спецификация, заключающаяся в решении двух основных задач:
а) выбор факторов, влияющих на исследуемую характеристику;
б) определение вида уравнения регрессии.
Второй этап – оценивание параметров уравнения.
Рассмотрим модель парной линейной регрессии.
Исходными данными для ее построения являются две совокупности наблюдений:
1) { х1, х2, …, хn }- значения независимого фактора х;
2) { у1, у2, …, уn } - значения исследуемой характеристики у для соответствующих значений х.
При этом для каждого i = 1,…,n
yi = α + βxi + εi,
где εi – i-я реализация случайного возмущения ε.
Относительно ε делаются следующие предположения:
1) ε – случайная величина, распределенная по нормальному закону;
2) М(ε) = 0; Д(ε) = const;
3) последовательные значения ε не зависят друг от друга.
Уравнение линейной регрессии ищется в виде
ŷ = а + bx
К параметрам а и b также предъявляются требования:
1) несмещенности, т.е. М(а) = α;
М(b) = β;
2) состоятельности, т.е.
Это значит, что с ростом числа наблюдений дисперсии оценок параметров стремятся к нулю;
4) эффективности – это значит, что оценки параметров имеют минимальную дисперсию по сравнению с любыми другими оценками данных параметров.
Оценки параметров уравнения регрессии можно получить с помощью метода наименьших квадратов (МНК), который заключается в минимизации суммы квадратов отклонений наблюдаемых значений исследуемой характеристики у от ее значения, рассчитанного по уравнению регрессии для того же значения х.
Для реализации этого метода построим функцию
Q(a,b) = 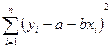
и потребуем ее минимизации, т.е. решим задачу на экстремум
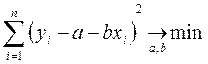
Для этого найдем частные производные
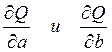
и приравняем их нулю. Получим следующую систему уравнений:
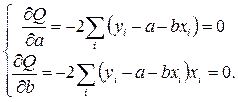
Сократим оба уравнения на (-2) и подействуем знаком суммы на каждое слагаемое отдельно. Затем перенесем отрицательные слагаемые в правую часть.
Получим систему нормальных уравнений для определения параметров a и b:
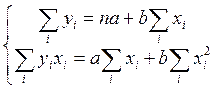
Решается эта система разными методами: подстановки, с помощью определителей и др.
В результате получим следующее решение:
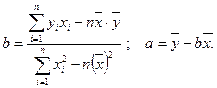
 2014-02-09
2014-02-09 1181
1181







