2014-02-09
685.
,,.
Прямое произведение матриц.
.
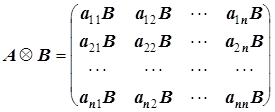Унитарная матрица.
Если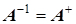 
, то матрица 
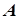- унитарная ее детерминант равен 1.
Унитарное преобразование матрицы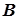 
: 
.
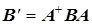Вращение вектора можно представить как произведение матриц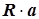 
, где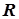 
- матрица преобразования координат; 
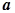- вектор-столбец исходных значений координат. В двухмерном случае поворот на угол Q задается матрицей:
.
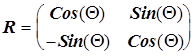Эта матрица определяет поворот вектора на угол Q по часовой стрелке или поворот системы координат против часовой стрелки. (Угол Q - положительный.)
Поворот, обратный данному, есть поворот на угол (-Q). Т.о. матрица
.
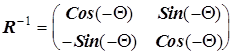Учитывая, что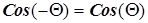 
и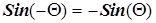 
получим
.
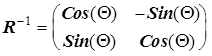Т.о.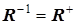 
, следовательно матрица 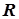- унитарная.
В трех измерениях матрица поворота имеет вид:
Третье измерение - ось поворота.
Операции симметрии.
Рассмотрим множество операций симметрии, используемых при описании молекул. Операция симметрии - действие при применении которого конфигурация объекта совпадает с первоначальной. Операция симметрии должна быть определена по отношению к элементу симметрии. Элемент симметрии - это геометрический объект, такой, как плоскость, линия, точка, относительно которого выполняет операция симметрии.
|
|
|
Существует пять различных типов элементов симметрии, которыми может обладать изолированный объект.
* Тождественная (или единичная) операция. Эта операция либо ничего не делает с системой, либо возвращает ее в исходное состояние (поворот на 360о).
* Ось вращения. Если поворот на угол 2p/n приводит к конфигурации совпадающей с исходной, то он называется поворотом типа Cn. Поворот осуществляется по часовой стрелке. Соответствующий элемент симметрии Cn - собственная ось поворота n -го порядка. Поворот на угол, кратный некоторому элементарному углу (т.е. на угол m2p/n), обозначается как Cnm. Если кратный поворот можно выразить через поворот более низкого порядка, то используется обозначение поворота низкого порядка. Многие системы обладают несколькими собственными осями симметрии. В этом случае ось наивысшего порядка называется главной осью. Если имеется несколько осей одного и того же порядка, то одну из них произвольно выбирают главной.
* Плоскость симметрии. Обозначение - s. Плоскости симметрии в зависимости от их связи с главной и вспомогательной осями разделяются на три типа. Существуют: вертикальная плоскость симметрии sv , содержащая главную ось; диэдральная плоскость симметрии sd , которая содержит главную ось и делит угол пополам между вспомогательными осями 2-го порядка, перпендикулярными к главной оси, или иногда содержит другие элементы; горизонтальная плоскость симметрии sh, перпендикулярная главной оси.
|
|
|
* Несобственная ось поворота или зеркально-поворотная ось n -го порядка. Обозначается как Sn. Представляет собой поворот относительно Cn с последующим отражением в горизонтальной плоскости sh, перпендикулярной этой оси. Элементы симметрии Cn и sh могут в отдельности не существовать.
* Точка инверсии (i). При отражении в этой точке любая точка пространства с координатами (x,y,z) переходит в точку с координатами (-x,-y,-z).
Лекция 2.
|
|
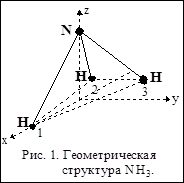
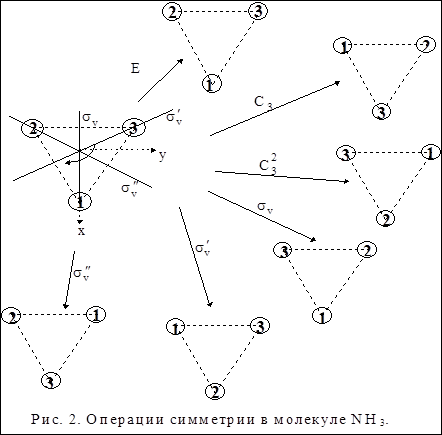
Рассмотрим операции симметрии на примере молекулы аммиака NH3. Геометрическое строение этой молекулы - тригональная пирамида, в основании которой лежат атомы водорода, образующие правильный треугольник. [Нарисовать структуру и пронумеровать атомы водорода как показано на рис. 1]. При операциях симметрии происходит взаимозамещение атомов водорода; атома азота остается неподвижным. Поэтому для иллюстрации операций симметрии рассмотрим только атомы водорода и для этого их пронумеруем (рис.1). [Далее подробно рассмотреть действие операций симметрии E, C3, C3 2, sv, sv¢, sv² в соответствии с рис. 2]. Оси поворота проходят по оси z, плоскости включают ось поворота и один из атомов водорода (см. рис. 2). Поворот - по часовой стрелке.
Используя рис. 2 можно легко определить результат последовательного выполнения (или произведения)двух операций симметрии. При этом расположение элементов симметрии (т.е. осей поворота и плоскостей) в декартовом пространстве остается неизменным. В итоге для рассматриваемого примера можно составить таблицу произведений операций симметрии (см. ниже).
Таблица 1. Произведения операций симметрии.
| E | C3 | C3 2 | sv | sv¢ | sv² | |
| E | E | C3 | C3 2 | sv | sv¢ | sv² |
| C3 | C3 | C3 2 | E | sv¢ | sv² | sv |
| C3 2 | C3 2 | E | C3 | sv² | sv | sv¢ |
| sv | sv | sv² | sv¢ | E | C3 2 | C3 |
| sv¢ | sv¢ | sv | sv² | C3 | E | C3 2 |
| sv² | sv² | sv¢ | sv | C3 2 | C3 | E |
Каждый элемент таблицы - результат последовательного выполнения 2-х операций симметрии. Первой выполняется операция соответствующая столбцу, второй - строке.
[Подробно рассмотреть построение таблицы на примере 2 и 4-го столбцов. Остальные столбцы могут быть заполнены самостоятельно. На примере таблицы показать, что операции симметрии молекулы NH3 удовлетворяют групповым теоремам.]
Групповые теоремы:
1. Произведение 2-х элементов дает третий элемент, также являющийся элементом группы.
2. Выполняется ассоциативный закон. Т.е. (ab)c=a(bc). Рассмотрим тройное произведение C3svC3 2:
(C3sv)C3 2 = sv¢ C3 2 = sv²
C3(svC3 2) = C3sv¢ = sv².
3. В группе есть элемент, коммутирующий с любым другим элементом и оставляющим его неизменным. Это единичный элемент. EA=AE=E.
4. Элемент, обратный к каждому элементу группы, также является элементом группы. Например: C3 C3 2 = C3 2 C3. Отражения в плоскости обратны сами себе.
Таким образом операции симметрии NH3 удовлетворяют групповым постулатам и составляют математическую группу. Аналогичная ситуация имеет место и для любых других систем. Группы, описывающие симметрию ядер молекулы, называются точечными, т.к. все элементы симметрии пересекаются, по крайней мере, в одной точке.
В приведенном выше примере, рассмотрим два элемента C3и svи найдем результаты произведения их друг с другом и самих на себя (см. табл. 1):
C3sv = sv¢; sv C3 = sv²; C3 C3 = C3 2 ; sv sv = Е.
Т.о. получены все элементы группы. Эти элементы называются генераторами группы. Полное число элементов в группе - порядок группы (в нашем примере порядок равен 6). В рассматриваемом примере операции C3и svне единственный набор генераторов. Это могут быть и пары (C3, sv¢), (C3, sv²), (C3 2 , sv), (C3 2 , sv¢) и (C3 2 , sv²). Однако обязательно должна быть одна из осей C3или C3 2 и одна из плоскостей sv, sv¢ или sv². Поэтому эту группы и обозначают как C3v. Элементы C3и C3 2 не порождают всю группу. Но они вместе с элементом Е порождают подгруппу точечной группы C3v. Подгруппа - множество элементов, удовлетворяющее групповым постулатам. [ Показать с использованием табл. 1, что элементы {Е, C3и C3 2 }составляют группу C3.] Кроме того, в группе C3v можно выделить еще три подгруппы {E, sv}, {E, sv¢ }и {E, sv² }полностью эквивалентные друг другу. Эти подгруппы называются циклическими, т.е. содержат степени одного и того же элемента. Единичный элемент в циклической группе также является степенью указанного элемента.
|
|
|
