Введение. Уравнения в частных производных

Уравнения в частных производных

Лекция №9

В физике, химии, биологии, социологии потребность в уравнениях в частных производных возникает при попытке описать динамику большого числа более или менее одинаковых дискретных объектов, входящих в некоторую системную целостность. Если количество таких дискретных объектом мало, то можно обойтись системой дифференциальных уравнений, в которой каждый дискретный объект описывается своей подсистемой обыкновенных дифференциальных уравнений.

В качестве примера можно привести модель хищник-жертва в математической биологии, когда хищник и жертва способны активно передвигаться, подобно тому, как передвигаются в водной среде планктонные организмы. Активное движение предполагает преследование хищником своей жертвы и, наоборот, убегание хищника от жертвы. В данном контексте оказалось возможным не только моделировать движение отдельных особей, но и описать динамику популяцию в целом. Поскольку количество планктона в океане это миллионы тонн, постольку описание предполагается в терминах плотностей биомасс отдельных видов. Следуя[1], можно привести следующие уравнения, описывающие динамику в пространстве и времени пары видов: одного вида 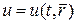хищника и одного вида 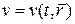жертвы:

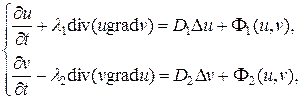(1)

где l ₁, l ₂ — параметры описывающие силы преследования и убегания, D ₁, D ₂ — коэффициенты диффузии, F₁, F₂ — члены ответственные за размножение жертвы, ее выедание хищником, и естественную смерть хищника.

Система уравнений (1) выведена из так называемого гидродинамического приближения, когда сообщество планктонных организмов рассматривается как сплошная среда. В качестве примера приведем уравнения, описывающие динамику вязкой несжимаемой жидкости:

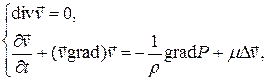(2)

где 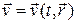— поле скорости, 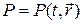— поле давления, r — плотность жидкости, m — кинематическая вязкость.

Наконец, приведем еще один пример уравнения теплопроводности, которое возникает в моделях сплошной среды для описания баланса тепла:

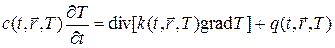, (3)

где 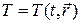— поле температуры, c — теплоемкость, k — коэффициент теплопроводности, q — плотность источников и стоков тепла.

К уравнениям в частных производных приводят задачи газовой динамики, гидродинамики, переноса излучения, теории упругости, описания электромагнитных полей, популяционной динамики, морфогенеза, математической экономики и во многих других задачах.

Из примеров (1) — (3) видно, что обычно в качестве независимых переменных выступает время t и пространство 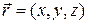, но могут быть и другие независимые переменные. Обычно решение ищется в некоторой области изменения независимых переменных 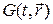. Для выделения единственного решения из некоторого семейства решений задают некоторые дополнительные условия, обычно формулируемые на границе области.

При изучении процессов во времени нас обычно интересуют решения на отрезке времени [ t ₀, t ₁], при этом область изменения независимых переменных может быть преобразована к виду:

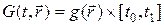. (4)

Согласно (4), решение определяется в области 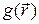на отрезке времени [ t ₀, t ₁], причем дополнительное условие, заданное при t = t ₀ называется начальными данными, а на границе области 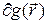— граничными или краевыми условиями.

Если в задаче определены только начальные данные, то ее называют задачей Коши. Так, для уравнения теплопроводности (3) в неограниченном пространстве можно сформулировать задачу с начальными данными

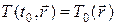. (5)

Известно, что если 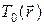— кусочно-непрерывная ограниченная функция, то решение задачи (3), (5) единственно в классе ограниченных функций.

Задачу с начальными и граничными условиями называют смешанной краевой задачей или нестационарной краевой задачей. Для смешаной задачи (3) дополнительные условия могут иметь, например, следующий вид:

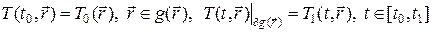. (6)

Часто постановка тех или иных физических задач приводит к ситуации, когда переходные процессы уже произошли и дальнейшая динамика отсутствует, т.е. зависимые переменные соответствующих уравнений не зависят от времени или являются стационарными. В этом случае задача формулируется в области 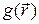, а дополнительные условия сводятся к краевым условиям на границе области .

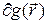Напомним известную классификацию уравнений в частных производных на примере одного уравнения, зависящего от двух переменных

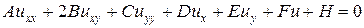. (7)

Если коэффициенты уравнения (7) не зависят от u, то уравнение является линейным, если коэффициенты являются константами — линейным уравнением с постоянными коэффициентами, если коэффициенты зависят от u, то уравнение (7) называется квазилинейным. Если A º B º C º 0. а D ¹ 0 и E ¹ 0, то уравнение (7) называется уравнением переноса и имеет первый порядок. Для уравнения второго порядка классификация определяется знаком дискриминанта B ² - AC. Для гиперболических уравнений дискриминант положителен, для параболических — равен нулю, для эллиптических уравнений — отрицателен.