Определение. Множество, равномощное множеству натуральных чисел 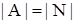 называется счетным.
называется счетным.
Примеры.
{0, 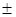 1,
1, 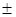 2,
2, 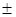 3,…}
3,…}
N = 1, 2, 3, 4, 5 A = 0, 1, -1, 2, -2, 3, -3
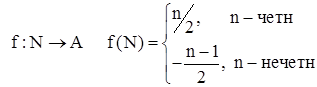
Теоремы о счетных множествах
Теорема 1. "¥ множество содержит счетное подмножество.
Док-во.
Выберем элемент a1ÎA (A не пусто, так как оно бесконечно);
выберем элемент a2ÎA\{a1} (A\{a1} не пусто, так как A бесконечно);
и т.д. В результате получим множество, каждому элементу которого сопоставлено натуральное число n.
Теорема 2. " ¥ подмножество B счетного множества A счетно.
Д-во. Согласно Т1 из ¥ множества B можно выделить счетное C.
Тогда CÍBÍA. В силу определения мощности |C|£|B|£|A|. Так как A и C – счетные, то |A|=|C|. Т. е. |A|£|B|£|A|. Отсюда следует, что |B|=|A|.
Тем самым, счетное множество равномощно своей ¥ части.
Т-ма 3. Объединение конечного или счетного семейства счетных множеств – есть счетное множество.
Доказательство. Пусть 
A1={a11,a12,…},
A2={a21,a22,…},
A3={a31,a32,a33,…},
………………..
An={an1,an2,an3,…,ann,…},
………………..
Расположим элементы A в следующем порядке
a11,a12,a21,a31,a22, a13,a14,a23,a32,a41,…
Тем самым, получили взаимно однозначное отображение N на A.
Если в множествах A1, A2, A3,… есть общие элементы, то их объединение A есть подмножество рассмотренной выше последовательности. Но согласно теореме 2 оно счетно.
Следствие 1. Если A и B счетные, то A x B – счетное.
Следствие 2. множество рациональных чисел – счетное
| 1/1 | 1/2 | 1/3 | 1/4 | |
| 2/1 | 2/2 | 2/3 | 2/4 | |
| 3/1 | 3/2 | 3/3 | 3/4 | |
| 4/1 | …. | …. | …. | |
| …. | …. | …. | …. |
Следующая теорема позволяет утверждать, что не существует «самого большого» по мощности множества.
Теорема. Мощность булеана множества всегда больше мощности самого множества, т.е |M|<|B(M)|.
Доказательство.
Так как MÍB(M), то |M|£|B(M)|.
Допустим, что |M|=|B(M)|. Значит, $ «соответствие f:M®B(M), т.е. каждому эл-ту xÎM поставлено в соответствие некоторое множество {xi1, xi2,…}=f(x). Возможны ситуации, когда xÎf(x) и когда xÏf(x).
Выделим множество P={x | xÏf(x)}. Тогда $ эл-т yÎM такой, что f(y)=P (поскольку соответствие f:M®B(M), между эл-тами x и подмнож-вами «, а B(M)- булеан, то каждому подмн-ву в том числе и P поставлен в соответствие некоторый эл-т yÎM).
Приведем это заключение к противоречию. Возможны два случая: либо yÎP, либо yÏP.
Пусть yÎP. Тогда по определению P yÏP. Противоречие.
Пусть yÏP. Поскольку в P входят все эл-ты xÏf(x), то yÎP. Опять противоречие.
Теорема доказана.
Теорема. Мощность булеана (множества-степени) счетного множества = мощности континуума: |P(N)|=| [0,1] |.
Доказательство.
Пусть 0,010…1… – запись любого числа из A=[0,1] в 2ой системе счисления.
Сопоставим этому числу подмножество N, состоящее из чисел, равных номерам разрядов, в которых записана единица. Этим устанавливается взаимно однозначное соответствие между B(N) и [0,1].
 2014-02-10
2014-02-10 451
451






