Погрешность дискретизации в цифровых измерительных приборах

Принимаются заявки на размещение рекламы.

КАИ

5-й факультет:

- Дипломы

- Курсовые проекты

- Курсовые работы

- Рефераты

- Тесты

- Справочная литература

Свои работы присылайте на e-mail: info@kai5.ru

Удачной сессии!

Пишите: admin@kai5.ru

icq # 330-803-890

= www.kai5.ru =

В основе работы цифровых приборов лежит преобразование измеряемой величины X в пропорциональный временной интервал 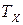, определяемый шириной одиночного прямоугольного импульса и дальнейшее определение длительности этого интервала времени. Определение длительности временного интервала происходит путем ее сравнения с периодом счетных импульсов 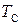. Прибор, подсчитывая количество счетных импульсов, попавших в этот временной интервал, определяет его длительность, а значит и измеряемую величину. Погрешность, связанная с неточностью определения длительности временного интервала называется погрешностью дискретности.

Рассмотрим два случая:

I. Начало временного интервала и счетных импульсов синхронизировано. Это означает, что первый счетный импульс и начало измеряемого временного интервала совпадают.

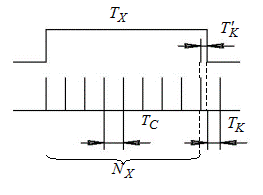
Рис. 1

На рис.1 видно, что при таком способе измерения длительности временного интервала появляется методическая погрешность, т.к. остается неучтенный остаток .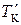

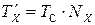(1)

В выражении (1) 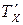— это временной интервал, являющийся аналоговой величиной, а величина 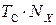, стоящая справа — дискретная величина. Из (1) следует, что число импульсов попавших в интервал 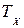равно

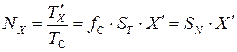(2)

В выражении (2) 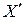— это измеряемая величина, 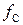— частота следования счетных импульсов, 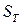— некоторый коэффициент преобразования измеряемой величины во временной интервал; 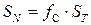, т. е. число сосчитанных импульсов пропорционально измеряемой величине. Из (2) следует:

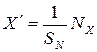, (3)

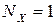Если , то 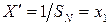— это минимально возможная измеряемая величина. С учетом этого (3) принимает вид

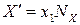(4)

При таком измерении появляется погрешность дискретности. 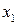— это шаг дискретизации. 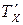— результат измерения реальной величины, который только приближенно совпадает с действительной величиной. 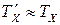; 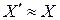. Таким образом действительное значение временного интервала равно:

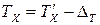, (5)

Из рис. 1 видно, что

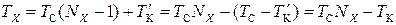(6)

В (6) 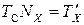,следовательно 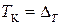— случайная погрешность (погрешность дискретизации), которая лежит в интервале 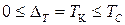. При этом закон распределения 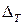равномерный. Погрешность дискретизации состоит из систематической и случайной части:

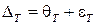(7)

В выражении (7) систематическая часть погрешности дискретизации 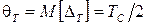. Граничные значения погрешности дискретизации:

,

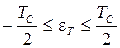Из выражения для СКО равномерного распределения 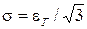следует, что СКО погрешности дискретизации будет 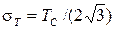или

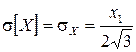(8)

Точность измерения также характеризует относительное среднеквадратическое отклонение. Оно является безразмерной величиной и равна

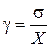(9)

ОСКО погрешности дискретизации можно получить подставив (8) в (9):

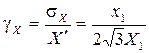, (10)

или

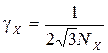(11)

Из (11) следует, что увеличение числа счетных импульсов приводит к уменьшению погрешности, т. е. ее можно регулировать. Рассмотренный случай относится к случаю, когда первый импульс считается, и число сосчитанных импульсов не совпадает с числом временных интервалов.

Пример: Пусть 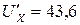В, тогда из (4) следует, что 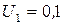В.

Рассмотрим случай, когда первый импульс не считается, тогда:

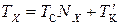, (12)

где 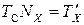, а 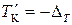. Погрешность дискретизации лежит в интервале 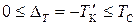, ее систематическая составляющая

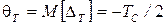
Таким образом погрешность дискретности противоположна по знаку первому случаю, т. е. изменилась только систематическая погрешность, случайная — не изменилась. Формулы (8) и (11) справедливы и для этого случая.