Icq # 330-803-890
Принимаются заявки на размещение рекламы.
Удачной сессии!
Тесты
Рефераты
Курсовые работы
Курсовые проекты
Дипломы
КАИ
Справочные материалы и Интернет-ресурсы
1. Российский статистический ежегодник. 2010г. (3,6 Мб) на сайте www.gks.ru. Приложение "Социально-экономические показатели Российской Федерации в 1991-2009 гг."
2. Институциональная экономика https://ie.boom.ru/1/index.htm
3. Журнал «Вопросы экономики» https://informag.mipt.rssi.ru/data/j112r.html
4. Журнал «Экономика и математические методы» https://www.cemi.rssi.ru/emm/home.htm
5. Журнал «Проблемы теории и практики управления» https://www.ptp.ru
6. Институт экономических проблем переходного периода https://www.iet.ru
7. Центральный экономико-математический институт https://www.cemi.rssi.ru
8. Центральный банк Российской Федерации https://www.cbr.ru
5-й факультет:
- Справочная литература
Свои работы присылайте на e-mail: info@kai5.ru
Пишите: admin@kai5.ru
= www.kai5.ru =
В практике измерений весьма часто приходится определять погрешность, которая определяется влиянием на результат измерения нескольких отдельных погрешностей.
Пусть искомый выходной измерительный сигнал 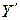 (например, результат косвенного измерения или выходная величина средства измерения) связана с некоторыми величинами
(например, результат косвенного измерения или выходная величина средства измерения) связана с некоторыми величинами 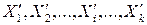 (аргументами) известной детерминированной функциональной зависимостью
(аргументами) известной детерминированной функциональной зависимостью
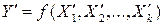 (1)
(1)
Учитывая, что 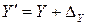 , (где
, (где 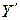 — истинное значение,
— истинное значение, 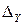 — результирующая погрешность),
— результирующая погрешность), 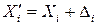 ,
, 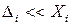 , разлагая функцию (1) в ряд Тейлора и пренебрегая членами со степенями выше первой, можно найти приближенное выражение:
, разлагая функцию (1) в ряд Тейлора и пренебрегая членами со степенями выше первой, можно найти приближенное выражение:
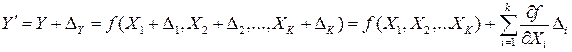 (2)
(2)
Принимая во внимание, что истинное значение величины 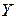
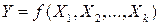 (3)
(3)
и вычитая (3) из (2), получим выражение для результирующей погрешности:
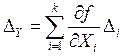 (4)
(4)
Обозначив 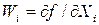 , получим
, получим
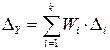 (5)
(5)
Где 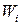 — весовые коэффициенты пересчета отдельных погрешностей в размерность искомой величины
— весовые коэффициенты пересчета отдельных погрешностей в размерность искомой величины 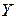 , которые учитывают степень влияния отдельных погрешностей
, которые учитывают степень влияния отдельных погрешностей 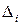 аргументов на общую погрешность
аргументов на общую погрешность 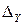 . Очевидно, что произведение
. Очевидно, что произведение 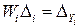 есть составляющая общей погрешности, вызванная погрешностью аргумента
есть составляющая общей погрешности, вызванная погрешностью аргумента 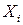 , т. е.
, т. е.
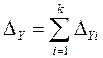 (6)
(6)
В общем случае каждая погрешность 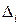 состоит из систематической
состоит из систематической 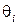 и случайной составляющей
и случайной составляющей 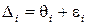 , и, следовательно
, и, следовательно
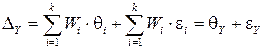 , (7)
, (7)
где
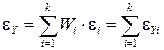 (8)
(8)
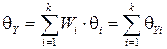 (9)
(9)
представляют собой случайную и систематическую составляющие общей погрешности 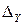 .
.
К сожалению, весьма простые формулы (4), (8) и (9) мало пригодны для практического использования, поскольку при этом нужно знать не только величину, но и знак (+ или –) погрешности каждого аргумента, которые, как известно, меняются и поэтому обычно неизвестны. Так что эти формулы фактически справедливы для конкретных реализаций погрешностей в отдельных измерениях.
 2014-02-10
2014-02-10 627
627






