Бесконечные цепочки

Если в схеме есть проводник, по которому не течет ток, то данный проводник можно удалить из этой схемы. Распределение оставшихся токов (а, следовательно, и сопротивление всей схемы), не изменятся.

2) Если в схеме есть две точки, при мысленном соединении которых проводником, ток через этот проводник не потечет, то эти точки можно соединить в одну («слить»). Распределение всех других токов в цепи не изменится.

В общем случае, найти такие проводники и точки сложно. Их может вообще не быть в схеме. Однако, если схема обладает симметрией, то этот поиск можно проводить по определенным правилам. Вообще, слово симметрия в физике, как и в математике, играет очень важную роль. Оно означает, что существует некий объект (например, электрическая схема) и некоторое его преобразование (поворот, зеркальное отражение..), которое сохраняет его вид, то есть, переводит его самого в себя. Если для нашей схемы мы нашли такое преобразование, то можем воспользоваться следующим правилом:

Если поменять полярность подключения источника (то есть, поменять «+» и «-» источника местами), то все токи в цепи сменят направление на противоположное, сохранив свои значения. Это станет довольно очевидным, если сообразить, что, изменив полярность источника, мы, фактически, мысленно изменили знак носителей электричества. А это означает, что их движение соответствует движению исходных носителей, только в другую сторону. То есть, ток при такой процедуре просто поменял направление, сохранив свою величину.

Тогда можно сделать следующий вывод.

1) Если наше преобразование симметрии переводит схему саму в себя, причем полярность подключения источника при этом сохраняется, то, обнаружив в схеме резисторы, ток через которые изменил направление на противоположное, можно смело утверждать, что ток через них не течет!

2) Если наше преобразование симметрии переводит схему саму в себя, причем полярность подключения источника при этом меняется на противоположную, то обнаружив в схеме резисторы, ток через которые не изменил направление, можно смело утверждать, что ток через них не течет!

Во всем этом разобраться довольно сложно, поэтому приведем несколько примеров

Пример № 1. Рассмотрим мостовую схему следующего вида

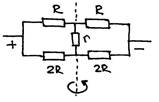
Видно, что схема переходит сама в себя при повороте на 180⁰ вокруг вертикальной оси. При этом токи, текущие через горизонтальные резисторы изменили свое направление на противоположное. Так и должно быть, ведь полярность подключения источника при нашем повороте изменилась на противоположную. А ток через резистор r не изменил своего направления! Значит, он равен нулю, и резистор r можно убрать из схемы, не изменив ее сопротивления и токи через горизонтальные резисторы. Дальше без труда рассчитываем сопротивление четырех резисторов. Оно равно 4R/3.

Пример № 2. Рассмотрим мостовую схему, изображенную на самом первом рисунке, при условии, что все сопротивления равны R. Видно, что у этой схемы есть еще одно преобразование симметрии - поворот на 180⁰ вокруг горизонтальной оси. При этом она переходит сама в себя, причем полярность подключения источника сохраняется. После такого поворота мы заметим, что токи через горизонтальные резисторы сохранили свою величину и направление (как и должно быть, ведь на изменилась ни схема, ни подключение источника), а ток через вертикальный резистор «перевернулся». Но он тоже должен сохранить свое направление! Значит, он равен нулю. Убираем его, и вычисляем полное сопротивление цепи, равное R. Замечу, что цепь из первого примера не обладает этой симметрией, так как не переходит в себя при повороте вокруг горизонтальной оси.

Пример № 3. Рассмотрим двенадцать резисторов R, спаянных в виде ребер куба. Присоединим контакты источника к концам любого резистора (на рисунке – к нижнему ребру). Найдем сопротивление цепи в этом случае.

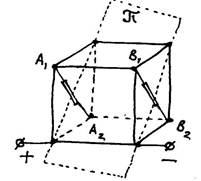
Обратим внимание на две пары точек А₁А₂ и В₁В₂. Видно, что они лежат симметрично относительно плоскости π, которая является плоскостью симметрии как цепи, так и подключения полюсов источника тока. Если бы между точками А₁А₂ (или В₁В₂) были бы подключены произвольные резисторы (они нарисованы), ток через них не протекал бы (доказательство как в примере 2). А значит пару точек А₁А₂ можно соединить в единую точку А (то же самое с точкой В). Тогда соединение проводников становится последовательно-параллельным и равно 7R/12. Вычислите его сами.

Преобразование «треугольник-звезда»

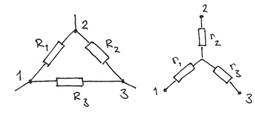
Одним из способов структурного преобразования электрической цепи является правило «треугольник-звезда», которое заключается в том, что соединение трех узлов резисторами R₁R₂R₃ в виде треугольника (рис. 1) можно заменить соединением этих же узлов звездой (рис. 2). Конечно, в звезде будут уже другие сопротивления r₁r₂r₃, отличающиеся от R₁R₂R₃. Однако, если подобрать r₁r₂r₃ так, чтобы между каждой парой узлов было то же полное сопротивление, что и в треугольнике, то внешняя цепь «не заметит разницы» в том, что происходит внутри этих трех узлов, а поэтому все внешние к этим узлам токи не изменятся.

Рассмотрим пару узлов 12. Между ними в треугольнике включено сопротивление R₁ и параллельно с ним два последовательных R₂R₃. Полное сопротивление между 12 в треугольнике равно 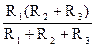, в звезде оно равно r₁+r₂. Составляем уравнение

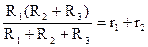, аналогично для двух других пар узлов

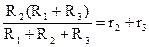и 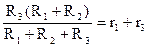решая эти три уравнения, можно легко получить выражения для r₁r₂r₃, и несколько сложнее для R₁R₂R₃.

Эти формулы сильно упрощаются, если какие-то сопротивления равны друг другу. Например, R₁=R₂=R, R₃=R₀. Тогда

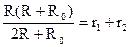
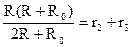
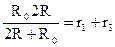
из первых двух уравнений видно, что r₁=r₃. Поэтому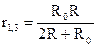

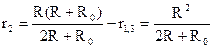Применим эти формулы к несимметричному мосту вида

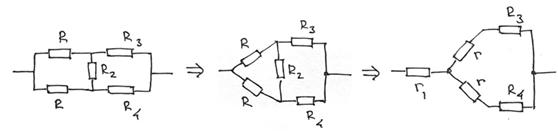
Видно, как треугольник трех левых резисторов преобразуется в звезду, причем

и Последняя схема представляет собой последовательно-параллельное соединение проводников.

Помимо реально существующих физических объектов и их моделей, иногда рассматриваются модели объектов, которые в реальности не могут существовать. Однако, математический анализ таких моделей может быть полезен. Примером служат бесконечные цепочки резисторов, спаянные из одинаковых звеньев.

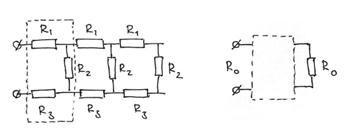
Видно, что данная цепочка обладает специфической симметрией. Добавление к ней еще одного элементарного звена (то есть, минимальной повторяющейся части, обозначенной на рисунке пунктиром), не меняет сам объект. Ни одна реальная цепь не может обладать таким свойством. Добавление чего-то всегда ее изменяет. Однако, легко заметить, что несмотря на бесконечное число элементов, полное сопротивление этой цепи будет конечным, а точнее, не превышающим величину R₁+R₂+R₃. Поскольку с R₂ запараллелено еще одно сопротивление, что делает полное сопротивление этой части меньше R₂. Кроме того, искомое сопротивление больше R₁+R₃, понятно по каким причинам. Метод вычисления искомого сопротивления R₀ ясен из правого рисунка. Добавление еще одного элементарного звена должно давать в итоге то же сопротивление R₀. 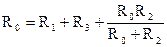. Решая это уравнение относительно неизвестного R₀, получим 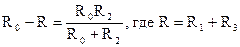тогда 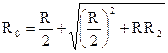. Видно, что данное выражение больше, чем 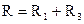, именно поэтому был взят знак + в корне. Чуть сложнее доказать, что это выражение меньше R₁+R₂+R₃. Сделайте это самостоятельно.