Экспериментов при ограничениях

Планирование экстремальных поисковых

Общие замечания

Сделаем несколько общих замечаний относительно рассмотренных выше методов поиска экстремума.

1. На точность выхода в область экстремума влияют помехи e, поэтому при приближении к экстремуму в случае статистического объекта рекомендуется выполнять параллельные опыты в намеченных точках факторного пространства (пробных и рабочих), что позволит точнее выделить приращения отклика в условиях помех, т.е. повысить точность нахождения экстремума.

2. Эффективность каждого из рассмотренных методов зависит от конкретных условий, в частности от формы поверхности отклика: крутая она или пологая, имеет ли ярко выраженные нарушения плавности (узкие гребни, овраги и т.д.). Искусство инженера - исследователя состоит в том, чтобы правильно подобрать метод поиска, наиболее подходящий для конкретных условий (форма поверхности отклика, уровень шумов, наличие ЭЦВМ и др.).

3. Если поверхность отклика имеет несколько экстремумов, то ни один из перечисленных методов не дает гарантии в том, что достигнут глобальный, а не локальный экстремум. Для уверенного нахождения глобального (т.е. главного, самого большого экстремума во всей области возможного изменения факторов) рекомендуется применять многократный поиск, причем каждый раз его следует начинать из различных участков факторного пространства. Если имеется возможность получить математическое описание высоких порядков для всей области допустимых значений или локальные математические описания, охватывающие всю эту область, то это может надежно решить вопрос, является ли найденный экстремум в действительности глобальным или лишь локальным.

4. На большинстве реальных объектов имеются ограничения, и в этих условиях применение методов поиска имеет свои особенности, о которых пойдет речь в следующем параграфе.

Большинство реальных объектов имеют два типа ограничений: факторные и функциональные. Факторными называют ограничения, накладываемые на входные переменные, т.е. ограничения типа

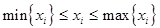(6.30)

(i - номер фактора; i = 1,2,..., n). Функциональными называют ограничения, накладываемые на целевые функции, характеризующие количественные или качественные стороны работы объекта:

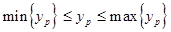, (6.31)

где p - номер отклика (выходной переменной). На рис. 6.8 приведен пример, когда на объекте присутствуют и факторные (по факторам х₁, х₂) и функциональные (по функциям отклика у₁, у_II) ограничения, причем для х₁ нижняя граница совпадает с нулевым значением этого фактора, основная функция отклика у₁ ограничена только снизу, а контролируемая функция отклика у_II ограничена только сверху. Примером факторного ограничения может служить ограничение скорости прокатки металла на прокатном стане: нижнее ограничение определяется плановым заданием и экономическими соображениями, верхнее - техническими возможностями электрических приводных двигателей, прочностью узлов прокатного стана и т.д. Примером функционального ограничения может служить выпуск заданного объема продукции из химического реактора: этот объем должен быть не ниже планового. При этом обычно существует дополнительное ограничение, например процент посторонних примесей в готовом продукте должна быть не выше допустимого.

Отметим, что если некоторые технологические процессы позволяют выходить за пределы области ограничений, хотя бы с целью изучения, то в других производственных процессах выход за эти пределы вызывает аварию (например, спекание катализатора, пределы вызывает аварию (например, спекание катализатора, взрыв и т.п.). В последнем случае особенно важно учитывать ограничения.

На рис. 6.8 концентрическими кривыми иллюстрируются линии постоянного уровня целевых функций:

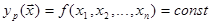, (6.32)

где р=I, II, а n=2. Штриховкой обозначены границы допустимой области W. Если экстремальная точка находится внутри этой области, то поисковые методы с учетом ограничений позволяют выйти в район этой точки. Если же экстремум находится вне области ограничений, как на рис. 6.8, то поисковыми методами в условиях ограничений можно найти лишь условный экстремум, под которым понимается наилучшее значение целевой функции на границе области ограничений. На рис. 6.8 это точка D в правом верхнем углу области ограничений W.

Рис. 6.8

Задача поисковой оптимизации при наличии ограничений формулируется так: с помощью целенаправленного поиска найти координаты максимума целевой функции у₁ внутри области ограничений W, определяемой неравенствами (6.30) и (6.31), т.е. 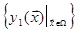. Для решения этой задачи используется модифицированный метод крутого восхождения. Очевидно, что при движении вдоль градиента К₀А, найденного по результатам ПФЭ вокруг базовой точки К₀ (рис. 6.8), можно дойти только до рабочей точки К₈, поскольку следующая рабочая точка К₉ лежит за пределами области ограничений. В таких условиях движение к максимуму производится по компромиссному направлению или вдоль границ допустимой области. Процедура модифицированного метода крутого восхождения заключается в следующем:

1. По уже известным правилам ПФЭ выбирают базовую точку, интервалы варьирования Dх_i (с учетом ограничений на факторы), ставят рандомизированные опыты. При этом кроме целевой функции у_I для контроля рекомендуется измерять и у_II.

2. По уже известным правилам метода крутого восхождения вычисляют оценки 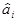коэффициентов для основных нормированных факторов z_i, производят их статистическое оценивание и определяют координаты рабочих точек К₅, К₆,... на направлении градиента К₀А (рис. 6.8).

3. Если функциональные ограничения в пробных опытах не нарушены, то ставят мысленные и реальные опыты в запланированных рабочих точках. Здесь имеются отличия от обычного метода крутого восхождения. Во-первых, реальные опыты при наличии ограничений должны ставиться чаще, чем без них. Во-вторых, во всех рабочих точках, кроме основной целевой функции у₁, обязательно выполняют измерения контролируемой целевой функции у_II. Если на направлении К₀А не встречаются границы допустимой области W, то рабочее движение осуществляют до частного экстремума на направлении градиента К₀А. Если же после очередной рабочей точки нащупано функциональное ограничение, то возвращаются к предыдущей рабочей точке.

4. Если частный экстремум достигнут, то эту точку принимают за новую базовую точку и переходят, как в обычном методе, ко второму циклу крутого восхождения. Если же встречается функциональное ограничение типа

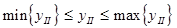, (6.33)

то за новую базовую точку принимают предыдущую рабочую точку, на один рабочий шаг (или несколько больше) удаленную от границы (6.33). В данном примере это точка К₇.

5. Вокруг новой базовой точки К₇ организуют новый ПФЭ (или ДФЭ), для чего выбирают новые, уменьшенные интервалы варьирования. При этом проявляют повышенное внимание к возможным нарушениям факторных и функциональных ограничений. В этом ПФЭ обязательно кроме у_I измеряют и контролируемую целевую функцию у_II.

6. По результатам рандомизированных опытов нового ПФЭ вычисляют и статистически проверяют оценк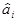и и 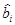коэффициентов для двух регрессионных моделей в нормированном масштабе:

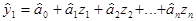, (6.34)

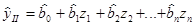. (6.35)

7. С помощью оценок 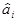определяют новое направление вектора градиента 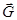основной оптимизируемой функции у₁, а с помощью оценок 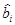находят направление вектор - нормали 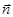к линиям постоянного уровня контролируемой целевой функции у_II. Практически в данном случае вектор -нормалью 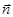служит вектор антиградиента у_II. Компромиссным вектором для продолжения движения к максимуму служит вектор 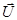(рис. 6.8), который является геометрической (векторной) суммой векторов 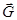и 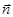, т.е. 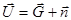. Для вычисления координат k-x рабочих точек в реальном масштабе на направлении компромиссного вектора 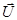можно использовать расчетную формулу

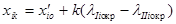, (6.36)

где l_Iiокр и l_Iiiокр - округленные по формуле (6.23) значения расчетных составляющих, соответственно l_Ii и l_Iii, которые, в свою очередь, вычисляются по уже известной формуле (6.22):

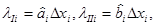
а 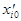- это i-я координата новой базовой точки (на рис. 6.8 точка К₇).

8. В рабочих точках на направлении вектора 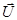ставят мысленные и реальные опыты, в которых получают расчетные и наблюдаемые значения как основной оптимизируемой функции у_I, так и контролируемой у_II.

9. Если на направлении вектора 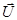(или на первоначальном направлении вектор -градиента К₀А) встречено факторное ограничение типа (6.30) (на рис. 6.8 точка С), то движение к экстремуму продолжают вдоль факторной границы max{x_i} (или min{x_i}), для чего координаты очередных рабочих точек вычисляют по формуле (6.36) для всех факторов, кроме х_i. Координаты этих рабочих точек по фактору х_i принимают равными

x_ik=max{x_i}=const или x_ik=min{x_i}=const (6.37)

в зависимости от конкретного случая. Если ограничение типа (6.30) записывается в виде min{x_i}<x_i<max{x_i}, то следует отступить от такой факторной границы на безопасное расстояние.

10. Движение к максимуму прекращают в одном из следующих случаев: а) достигнут частный экстремум при движении вдоль факторной границы при одном из условий (6.37); б) встречена вторая факторная граница (этот случай иллюстрируется точкой D на рис. 6.8); в) при движении вдоль факторной границы встречено функциональное ограничение по контролируемой целевой функции у_II (точки Е и F). Во всех этих случаях оказывается достигнутым условный экстремум. Если же на очередном цикле крутого восхождения внутри области W по результатам пробных опытов ПФЭ все оценки 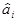оказываются статистически незначимыми, т.е. grad y_I»0, то считается достигнутым безусловный экстремум. Однако поскольку достигнутый экстремум (условный или безусловный) может оказаться лишь локальным, поиск следует повторить из другой базовой точки, выбранной в противоположной стороне области ограничений по сравнению с начальной базовой точкой К₀ или выбранной случайным образом.

ЛИТЕРАТУРА

1. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий - М.: Наука, 1976.

2. Дэниел К. Применение статистики в промышленном эксперименте. - М.: Мир, 1979.

3. Зуховицкий С.И., Авдеева Л.И. Линейное и выпуклое программирование. - М.: Наука, 1964, 1967.

4. Математическое описание и оптимизация многофакторных процессов/Под ред. Г.К.Круга.- Труды МЭИ, 1966, вып. 67.

5. Налимов В.В., Чернова Н.А. Статистические методы планирования экстремальных экспериментов. - М.: Наука, 1965.

6. Растригин Л.А. Статистические методы поиска. - М.: Наука, 1968.

7. Химмельблау Д.М. Прикладное нелинейное программирование. - М.: Мир, 1975.