Доказательство.
В качестве функции 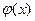 рассмотрим:
рассмотрим:
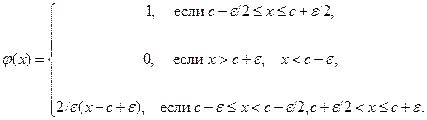
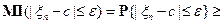
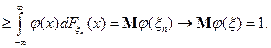
Следовательно, 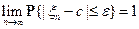 , т.е.
, т.е. 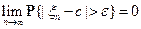 .
.
Определение. Распределения 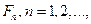 слабо сходятся к распределению
слабо сходятся к распределению 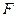 , если для любой непрерывной, ограниченой функции
, если для любой непрерывной, ограниченой функции 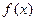
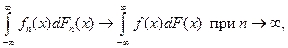
т.е. 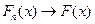 во всех точках непрерывности
во всех точках непрерывности 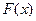 .
.
Обозначения:  ,
, 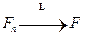 .
.
Теорема непрерывности. Пусть 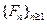 – последовательность функций распределения
– последовательность функций распределения 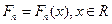 , и
, и 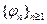 – последовательность соответствующих характеристических функций
– последовательность соответствующих характеристических функций
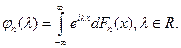
1)Если  , где
, где 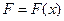 – некоторая функция распределения, то
– некоторая функция распределения, то 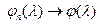 ,
, 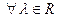 , где
, где 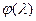 – характеристическая функция
– характеристическая функция 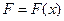
2)Если для любого 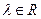 существует
существует 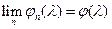 , и
, и 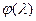 – непрерывна в точке
– непрерывна в точке 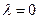 , то
, то 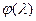 – характеристическая функция некоторого распределения
– характеристическая функция некоторого распределения 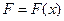 , и
, и 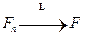 .
.
Доказательство 1) очевидно следует из определения слабой сходимости, примененного к функциям 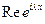 и
и 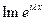 .
.
 2014-02-12
2014-02-12 488
488






