Пример 4. Найти оптимальные стратегии игры «Поиск» размера 2×2 (см

Найти оптимальные стратегии игры «Поиск» размера 2×2 (см. пример1).

Решение.

Игра "Поиск" задана платежной матрицей:

.

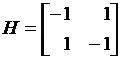Нижняя и верхняя цены игры соответственно равны α=-1 и β=1 (см. пример 2), т.е. игра не имеет седловой точки. Поэтому оптимальные стратегии игры будем искать в смешанных стратегиях.

Для игрока А средний выигрыш равен цене игры v (при B₁ и B₂); для игрока В средний проигрыш равен цене игры v (при A₁ и А ₂).

Системы уравнений в данном случае имеют вид:

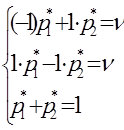
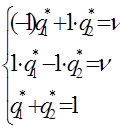
Решая эти системы, получим р^*₁=р^*₂=q^*₁=q^*₂=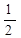, v=0.

Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждое из убежищ с вероятностью 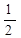, при этом средний выигрыш равен 0.

1.9 Геометрическая интерпретация игры 2×2

Решение игры 2×2 допускает наглядную геометрическую интерпретацию.

Пусть игра задана платежной матрицей Н=[hij], где i,j = 1,2.

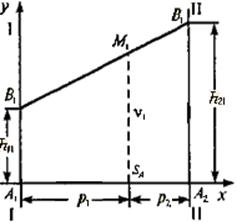
По оси абсцисс (рисунок 4) отложим единичный отрезок A₁A_2. Точка A₁(х=0) изображает стратегию A₁, а все промежуточные точки этого отрезка - смешанные стратегии S_A первого игрока, причем расстояние от S_A до правого конца отрезка - это вероятность p₁ стратегии A₁, расстояние до левого конца - вероятность p₂ стратегии A₂.

На перпендикулярных осях I—I и II—II откладываем выигрыши при стратегиях A₁ и A₂ соответственно. Если 2-й игрок примет стратегию B₁, то она дает выигрыши h₁₁ и h₂₁ на осях I—I и II—II, соответствующие стратегиям A₁ и A₂. Обозначим эти точки на осях I—I и II—II буквой B₁. Средний выигрыш v ₁, соответствующий смешанной стратегии S_A, определяется по формуле математического ожидания v ₁ = h₁₁ p₁ + h₂₁ p₂ и равен ординате точки M₁, которая лежит на отрезке B₁ B₁ и имеет абсциссу S_A (рисунок 4).

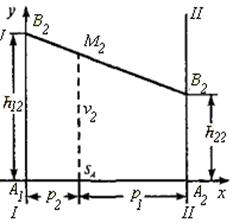
Рисунок 4	Рисунок 5

Аналогично строим отрезок B₂B₂, соответствующий применению вторым игроком стратегии B₂ (рисунок 5).

При этом средний выигрыш ν₂ =h₁₂ p₁ + h₂₂ p₂ - ордината точки M₂.

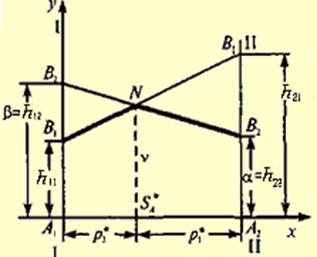
В соответствии с принципом минимакса оптимальная стратегия S*_A такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной (рисунок 6), показывают минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке B₁N - против стратегии B₁ , на участке NB₂ - против стратегии B₂).

Оптимальную стратегию S*_A = (p*₁ p*₂) определяет точка N, в которой минимальный выигрыш достигает максимума; ее ордината равна цене игры v. На рисунке 6 обозначены также верхняя и нижняя цены игры α и β.

Пусть Н=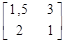

Определим оптимальную стратегию игрока А геометрическим методом

Откладываем по оси абсцисс (рисунок 7) единичный отрезок A₁A₂.

На вертикальной оси I-I откладываем отрезки: h₁₁, соответствующий стратегии B₁, и h₁₂, соответствующий стратегии B₂.

На вертикальной оси II—II отрезок h₂₁ соответствует стратегии B₁ , отрезок h₂₂ соответствует стратегии B₂ (рисунок 7).

Нижняя цена игры α=h₂₂ – наибольшему из наименьших.

Верхняя цена игры β =h₁₂ ( наименьшему из наибольших ), в нашем случае на графике показано, что седловая точка отсутствует. Из рисунка 7 видно, что

· абсцисса точки N определяет оптимальную стратегию S*_A,

· ордината — цену игры v.

Точка N является точкой пересечения прямых B₁B₁ и B₂B₂.

Рисунок 6	Рисунок 7

Уравнение прямой B₁B₁, проходящей через точки (0; h₁₁) и (1; h₂₁):

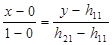или y = х(h₂₁-h₁₁)+h₁₁.

Уравнение прямой B₂B₂, проходящей через точки (0; h₁₂) и (1; h₂₂):

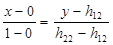или y = х(h₂₂-h₁₂)+h₁₂.

Точка пересечения прямых является решением системы:

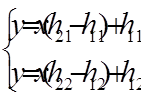
Решив систему, можно найти x и y, т.е. координаты точки N(х; у)

Тогда p*₂= х, p*₁= 1 - х;

оптимальная стратегия S*_A = (1-х; х),

цена игры v = у

Определение оптимальной стратегии игрока В.

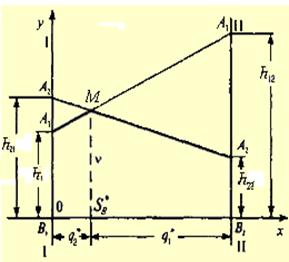
Оптимальную стратегию игрока В геометрически можно определить, если поменять местами игроков А и В и вместо максимума нижней границы A₂MA₁ в соответствии с принципом минимакса рассмотреть минимум верхней границы.

Абсцисса точки М определяет q*₂ в оптимальной стратегии игрока В, ордината этой точки — цена игры.

Прямая A₁A₁, проходящая через точки (0; h₁₁) и (1; h₁₂), удовлетворяет уравнению y = х(h₁₂-h₁₁)+h₁₁.

Прямая A₂A₂, проходящая через точки (0; h₂₁) и (1; h₂₂), удовлетворяет уравнению у = х(h₂₂-h₂₁)+h₂₁.

Координаты их точки пересечения М - это решение системы уравнений:

.

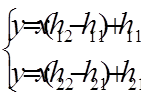Откуда найдем x и y М(х; у)

q*₂= х, q*₁= 1 - х

v = y S*_B = (1-х; х)

Оптимальное решение игры найдено.

Из решения задачи следует, что геометрически можно определять оптимальную стратегию как игрока А, так и игрока В, в обоих случаях используется принцип минимакса, но во втором случае строится не нижняя, а верхняя граница выигрыша и на ней определяется не максимум, а минимум.

Если платежная матрица содержит отрицательные числа, то для графического решения задачи лучше перейти к новой матрице с неотрицательными элементами; для этого к элементам исходной матрицы достаточно добавить соответствующее положительное число. Решение игры при этом не изменится, а цена игры увеличится на это число.

В примере 4 платежная матрица не имела седловой точки (α ≠β).

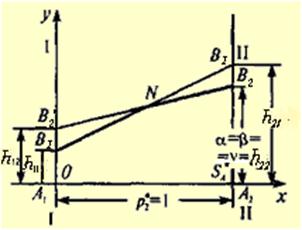
При наличии седловой точки графическое решение дают варианты, изображенные на рисунке 8 и 9. На рисунке 8 наибольшей ординатой на ломаной B₁NB₂ обладает точка B₂, поэтому оптимальной является чистая стратегия A₂ для игрока А (B₂ - для игрока В), т.е. оптимальное решение:

S*_A = (0;1), S*_B = (0;1).

Игра имеет седловую точку h₂₂ = v.

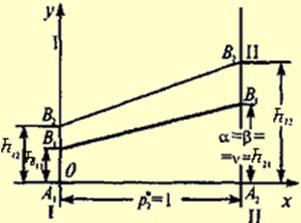
Рисунок 8	Рисунок 9

Чистая стратегия B₂ (рисунок 9) не выгодна для игрока В, поскольку при любой стратегии игрока А она дает последнему больший выигрыш, чем чистая стратегия B₁.

На основании принципа минимакса выделим прямую B₁B₁ и на ней точку B₁ с наибольшей ординатой на оси I-I. Чистая стратегия A₂ является оптимальной для игрока А, а чистая стратегия B₁ - для игрока В.

Оптимальное решение: S*_A = (0;1), S*_B = (1;0),

цена игры v = h₂₁ = α = β, т.е. имеется седловая точка.

Замечание:

графический метод можно применять при решении игры 2 × n и m × 2.