Основные растровые алгоритмы

Применяемые в настоящее время устройства вывода графической информации (мониторы, принтеры) по своей природе являются растровыми - изображение в них создается из отдельных точек. Поэтому даже при использовании векторной графики при выводе изображения на экран нужно определить, у каких точек изменить цвет, чтобы на экране отрисовался, к примеру, отрезок. Точнее говоря, заданному отрезку нужно поставить в соответствие множество на целочисленной плоскости, которое является достаточно точным приближением этого отрезка.

Данная процедура неоднозначна, так как "достаточно точно" можно понимать по-разному. Кроме того, алгоритмы визуализации графических примитивов должны быть простыми и работать исключительно быстро, поскольку иначе теряется преимущество векторной графики - малый объем занимаемой памяти и, соответственно, высокая скорость обработки.

Рассмотрим растровое отображение простейшей фигуры – отрезка. Процесс последовательной смены цвета множества пикселов, изображающих отрезок, называется растровой разверткой отрезка.

Простейшее решение состоит в следующем: по координатам отрезка получить уравнение прямой и, подставляя в него целочисленные значения координат, менять цвет у получающихся точек. Если концы отрезка имеют координаты (x₁, y₁) и (x₂, y₂), то отрезок задается уравнением:

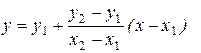(9)

При этом x меняется от x₁ до x₂. Напишем простейшую процедуру построения отрезка:

dY:=ABS(Y2-Y1)/(X2-X1));

y:=y1;

for x:=x1 to x2 do

begin

PutPixel(x, round(y));

y:=y+dy

end;

К сожалению, если отрезок не параллелен координатным осям, при таком построении он распадается на множество несоприкасающихся между собой пикселов и уже не выглядит как единый объект. Поэтому реально применяются два других способа визуализации отрезка, получивших название четырехсвязной и восьмисвязной разверток (Рис. 10.1).

а) б)

Рис. 8.7 - Четырехсвязная (а) и восьмисвязная (б) развертки отрезка.

Четырехсвязная разверткаотрезка включает те и только те точки, квадратные окрестности которых пересекаются с отрезком. Восьмисвязная разверткаотрезка включает те и только те точки, боковые стороны квадратных окрестностей которых пересекаются с отрезком.

Приведем алгоритм для генерации четырехсвязной развертки:

x:=x1;

y:=y1;

n:=x2-x1;

m:=y2-y1;

d:=(m/n);

e:=d/2;

for i:=1 to n+m do

begin

x:=x+1;

e:=e+d; { отклонение }

if e>0.5 then

begin

y:=y+1;

e:=e-1

end

else

begin

x:=x+1;

e:=e+d

end;

PutPixel(x,y)

end;

Здесь в переменной е хранится разница между координатой Y текущей точки отрезка и координатой Y точки пересечения отрезка с правой границей квадратной окрестности текущей точки растровой развертки. При e£0.5 отрезок пересекает окрестность точки, лежащей справа от текущей, и нужно сместиться вправо. При e£0.5 отрезок пересекает окрестность точки, лежащей выше текущей, и надо сместиться вверх (Рис. 10.2).

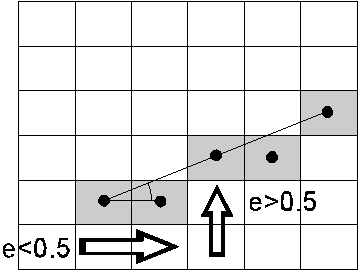
Рис. 8.8 – Схема работы алгоритма четырехсвязной развертки отрезка.

Как указывалось выше, очень важна эффективность алгоритма развертки. Как известно, компьютер работает с целыми числами гораздо быстрее, чем с вещественными. Поэтому было бы очень желательно придумать такой алгоритм растровой развертки, который использовал бы только целые числа. Целочисленные алгоритмы для развертки графических примитивов были разработаны инженером компании IBM Брезэнхемом и носят его имя.

Ниже приведена процедура на языке Паскаль, реализующая алгоритм Брезенхема для восьмисвязной развертки отрезка.

Procedure Bresenham(x1,y1,x2,y2,Color: integer);

var

dx,dy,incr1,incr2,d,x,y,xend: integer;

begin

dx:= ABS(x2-x1);

dy:= Abs(y2-y1);

d:=2*dy-dx; {начальное значение для d}

incr1:=2*dy; {приращение для d<0}

incr2:=2*(dy-dx); {приращение для d>=0}

if x1>x2 then {начинаем с точки с меньшим знач. x}

begin

x:=x2;

y:=y2;

xend:=x1;

end

else

begin

x:=x1;

y:=y1;

xend:=x2;

end;

PutPixel(x,y,Color); {первая точка отрезка}

While x<xend do

begin

x:=x+1;

if d<0 then

d:=d+incr1 {выбираем нижнюю точку}

else

begin

y:=y+1;

d:=d+incr2; {выбираем верхнюю точку, y-возрастает}

end;

PutPixel(x,y,Color);

end;{while}

end;{procedure}

Еще одна задача, часто решаемая в ходе визуализации – заливка цветом некоторой заданной границей области. Область обычно задается или в векторном виде массивом координат вершин многоугольника, или в растровом – набором пикселов определенного цвета, образующих замкнутый контур.

Для решения задачи заливки векторного многоугольника необходимо закрашивать тем или иным цветом выводимые на экран пиксели в зависимости от того, лежат они внутри многоугольника или снаружи. Таким образом, задача векторной заливки сводится к задаче определения принадлежности точки P(x,y) многоугольнику, заданному координатами вершин. Идея алгоритма для решения этой задачи состоит в следующем (Рис. 10.3).

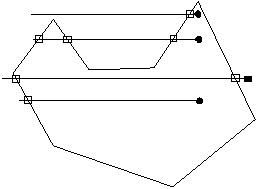
Рис. 8.9 –Определение принадлежности точки многоугольнику.

Проведем через точку P горизонтальную полупрямую (луч) и определим число пересечений этой полупрямой с ребрами многоугольника. Если это число нечетно, то точка Р лежит внутри многоугольника, четно – снаружи.

Заполнение растровой областихорошо знакомо программистам, поскольку почти во всех языках программирования есть соответствующие команды (например, в языке Pascal это команда FloodFill, в Delphi – метод FloodFill объекта TCanvas и т.д.)

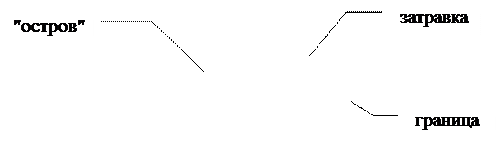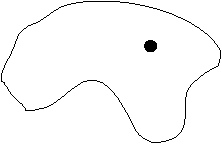
Рис. 8.10 – Заполнение растровой областис затравкой.

Граница области является четырех- или восьмисвязной растровой кривой, все пикселы которой имеют один и тот же цвет. Внутри области могут находиться "острова", которые закрашивать не надо. Предполагается, что внутри области задана точка начала закраски, называемая затравкой(Рис. 10.4).

Для выполнения заливки используется специальная структура данных, называемая стеком(stack). Стек работает по принципу "первым вошел – последним вышел" (Рис. 10.5).

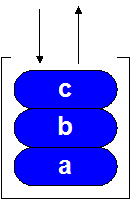
Рис. 8.11 - Стек.

Хорошим аналогом стека является магазин автомата Калашникова (программистская шутка гласит, что АКМ – лучшее средство для превращения стека в очередь). При извлечении значений из стека нужно помнить о том, что теперь они будут идти в обратном порядке. Если мы занесли в стек сначала а, потом b, потом c, то первым извлечется с, затем b и, наконец, а.

Эффективный алгоритм заливки основан на построчном сканировании заполняемой области. Вот его схема:

Инициализируем стек, помещая в него координаты затравочного пиксела. Пока стек не пуст:

извлекаем пиксел (х,у) из стека;

заполняем максимально возможный интервал, в котором находится пиксел, вправо и влево вплоть до достижения граничных пикселов;

запоминаем крайнюю левую Lx и крайнюю правую Rx абсциссы заполненного интервала;

в соседних строках над и под интервалом (Lx,Rx) находим незаполненные к настоящему моменту внутренние пикселы области, которые, как мы уже заметили, объединены в интервалы, а в каждом из этих интервалов находим крайние правые пикселы. Каждый из этих пикселов вносим в стек в качестве затравочного.

Такой алгоритм правильно заполняет область любой конфигурации, в том числе и с "островами" внутри.