Существуют три правила, которые часто используются. Эти правила практически самоочевидны, и они одинаково применимы для дискретных и непрерывных случайных переменных.
Правило 1. Математическое ожидание суммы нескольких переменных равно сумме их математических ожиданий. Например, если имеются три случайные переменные 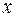 ,
, 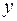 и
и 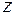 , то
, то
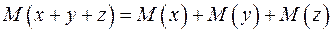 . (A.4)
. (A.4)
Правило 2. Если случайная переменная умножается на константу, то ее математическое ожидание умножается на ту же константу. Если 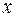 – случайная переменная и
– случайная переменная и 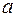 – константа, то
– константа, то
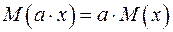 . (A.5)
. (A.5)
Правило 3. Математическое ожидание константы есть она сама. Например, если 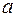 – константа, то
– константа, то
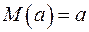 . (A.6)
. (A.6)
Следствие из трех правил:
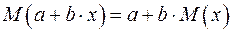 .
.
Независимость случайных переменных
Две случайные переменные 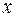 и
и 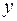 называются независимыми, если
называются независимыми, если
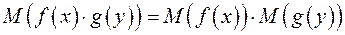 (A.7)
(A.7)
для любых функций 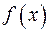 и
и 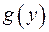 . Из независимости следует как важный частный случай, что
. Из независимости следует как важный частный случай, что 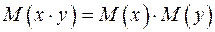 .
.
 2014-02-09
2014-02-09 551
551








