2014-02-12
221ТЕРМОДИНАМИЧЕСКИМИ ФУНКЦИЯМИ И ПАРАМЕТРАМИ
ВЗАИМОСВЯЗЬ ЭНЕРГИИ ГЕЛЬМГОЛЬЦА С ДРУГИМИ
1) продифференцируем уравнение (76):
.
Подставим в полученное уравнение вместо 
его значение из уравнения (71), получим:
;
.
Поскольку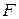 
изменяется при изменении объема и температуры, то есть 
, то 
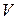и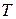 
называют собственными параметрами состояния системы для свободной энергии Гельмгольца.
Если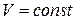 
: 
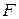уравнение устанавливает связь с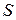 
;
: 
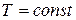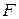уравнение устанавливает связь с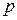 
.
Функцию, производная которой выражает другую термодинамическую функцию или параметр состояния, называют характеристической функцией.
Таким образом, свободная энергия Гельмгольца является характеристической функцией.
2) применим теперь уравнение (76) к начальному (1) и конечному (2) состояниям системы в каком-либо изохорно-изотермическом процессе:
; 
.
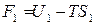Вычтем почленно, получим:
(78) уравнение Гиббса – Гельмгольца, позволяющее определить возможность протекания изохорно-изотермического процесса
Перепишем уравнение Гиббса – Гельмгольца (78) в виде:
|
|
|
,
подставим вместо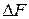 
, 
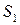и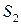 
их значения:
; 
; 
.
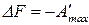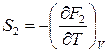После подстановки, получим:
(79) уравнение максимальной работы Гиббса – Гельмгольца
В уравнении (79): 
– тепловой эффект изохорно-изотермического процесса – и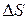 
– легко рассчитываются.
Следовательно, подставляя их значения в уравнение можно определить идет реакция или нет. Максимально возможный выход будет при равновесии.
Когда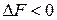 
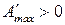
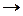прямой ход реакции;
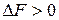
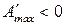
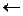обратный ход реакции;
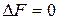
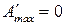
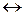термодинамическое равновесие.
4. 
(изобарно-изотермический процесс) (их большинство)
Для анализа воспользуемся выражением (74), получим:
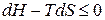или 
;
;
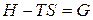. (80)
Функция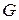 
обладает всеми свойствами термодинамической функции состояния. 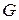– энергия Гиббса (свободная энтальпия) – пятая термодинамическая функций состояния.
Получаем:
.
Знак неравенства характеризует условие самопроизвольного (необратимого) протекания изобарно-изотермического процесса. Как видно, таким условием является убыль энергии Гиббса.
(
).
Равновесие в системе при изохорно-изотермических условиях устанавливается при минимальном значении энергия Гиббса. Условием минимума функции и, следовательно, равновесия является:
.
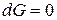Применим теперь к анализу обратимого изобарно-изотермического процесса уравнение (71), получим:
.
После интегрирования имеем:
. (81)
Как видим, убыль энергии Гиббса в изобарно-изотермическом процессе характеризует его максимальную работу.
Таким образом, энергия Гиббса является изобарно-изотермическим термодинамическим потенциалом.
