Логическое следствие

Определение. Формула B есть логическое следствие формул A₁, A₂,.., A_n, если формула B принимает истинное значение при тех же значениях, при которых истинна каждая из формул A₁, A₂,.., A_n.

Запись (A₁, A₂,.., A_n)ÞB означает, что B – логическое следствие формул A₁, A₂,.., A_n.

Пример. (A®B, A®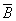)Þ.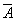

Докажем данное следствие.

A	B	A®B		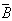A®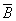
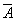
И	И	И	Л	Л	Л
И	Л	Л	И	И	Л
Л	И	И	Л	И	И
Л	Л	И	И	И	И

Из определения следует, что противоречие логически влечет любую формулу, а тавтология логически следует из любой формулы логики.

Определение. Формулы F и G называются равносильными, если они являются логическими следствиями друг друга. Обозначение: .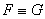

Проанализировав последнее определение, получаем, что формулы равносильны, если они на всех наборах значений переменных превращаются в одинаковые по истинностному значению высказывания.

Следующие теоремы связывают логическое следствие и импликацию, равносильность и эквиваленцию.

Теорема₁. 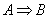тогда и только тогда, когда A®B – тавтология.

Теорема₂. 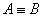тогда и только тогда, когда A«B – тавтология.