2014-02-12
1851
Выше был изложен алгоритм получения допустимого базисного решения в случае, когда первоначальное базисное решение недопустимо. Однако при расчете с помощью симплекс-таблиц удобнее пользоваться методом искусственного базиса. Он заключается в следующем.
Рассмотрим ЗЛП в каноническом виде:
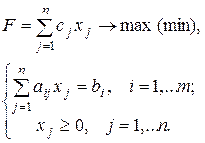(2.7)
Без ограничения общности можно считать, что все 
. В противном случае умножим соответствующее уравнение на –1. В каждое уравнение введем со знаком «+» свою неотрицательную переменную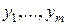 
, и рассмотрим вспомогательную задачу линейного программирования:
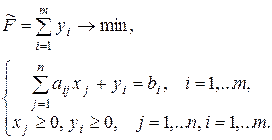(2.8)
Отметим, что решение задачи (2.8) всегда существует, т.к. ее множество допустимых значений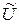 
непусто (
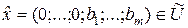), а целевая функция ограничена снизу (
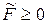). Решим задачу (2.8) симплекс-методом.
Возможны следующие случаи.
1. 
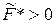. Тогда можно показать, что допустимое множество исходной задачи (2.7) пусто, т.е. эта задача не имеет решения.
2. 
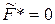, и минимум целевой функции 
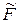достигается в угловой точке
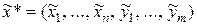(2.9)
допустимой области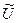 
вспомогательной задачи. Тогда
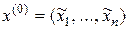(2.10)
угловая точка допустимого множества исходной задачи, и ее можно использовать в качестве начальной угловой точки при решении задачи (2.7) симплекс-методом.
Очевидно, что 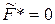тогда и только тогда, когда все 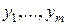равны нулю. Если задача (2.8) невырождена, это означает, что переменные 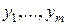являются свободными для угловой точки (2.9). Опустим столбцы, соответствующие этим переменным в окончательной симплекс-таблице, составленной при решении задачи (2.8). Полученная в результате этого таблица будет соответствовать системе ограничений задачи (2.7), разрешенной относительно переменных, являющихся базисными для угловой точки (2.9). Поэтому остается заменить в этой таблице последнюю строку на строку коэффициентов целевой функции исходной задачи, выраженной через свободные переменные, и продолжить ее решение симплекс-методом, выбрав точку (2.10) в качестве начальной угловой точки.
Если вспомогательная задача (2.8) вырождена, то некоторые из переменных 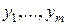могут оказаться базисными. Тогда эти переменные следует перевести в свободные с помощью холостых шагов симплекс-метода (см. п. 2.3). После этого исходная задача (2.7) решается, как описано выше.
Замечание 1. Столбцы симплекс-таблицы, соответствующие вспомогательным переменным 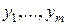, удобно вычеркивать на каждом шаге вместо того, чтобы исключать их одновременно в окончательной симплекс-таблице.
Замечание 2. Вспомогательные переменные можно вводить не во все ограничения задачи (2.7), а только в те из них, которые определяют недопустимые (отрицательные) компоненты базисного решения.
Пример 2.7. Методом искусственного базиса найти угловую точку допустимого множества следующей ЗЛП (пример 2.2):
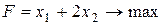
при ограничениях
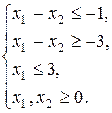
Решение. Приведем ЗЛП к каноническому виду:
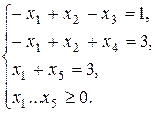
Первое уравнение определяет отрицательную компоненту базисного решения. Введем в него искусственную переменную у и составим вспомогательную ЗЛП:
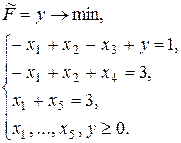
Базисные переменные: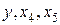 
. Свободные переменные: 
.
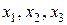Выразим 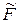через свободные переменные 
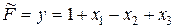и составим симплекс-таблицу:
 |  |  |  | |  | | | ||||
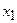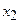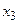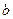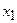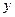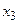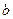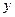| | -1 | -1 | 1:1=1 | 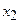| -1 | -1 | |||||
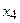 | -1 | 3:1=3 | ® | 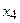| -1 | ||||||
 | | ||||||||||
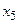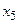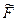 | 1 | -1 | 1 | -1 | 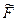| 0 | 0 | 0 |
Исключая вспомогательную переменную, получаем таблицу:
| | | | |
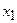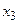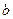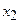| | -1 | -1 | |
| | |||
| | |||
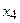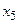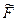| | 0 | 0 | 0 |
В нижней строке таблицы нет отрицательных элементов, а в правом нижнем углу стоит 0. Следовательно, минимум вспомогательной функции достигнут, и точка (0; 1; 0; 2; 3) есть допустимая угловая точка исходной задачи.
Выражаем базисные переменные и целевую функцию через свободные переменные:
.
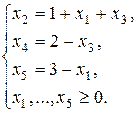
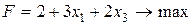Записывая коэффициенты целевой функции в последнюю строку получившейся таблицы, получаем симплекс-таблицу:
 |  |  | |
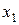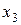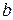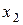 | -1 | -1 | |
 | |||
 | |||
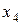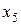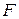 | 3 | 2 | -2 |
Теперь можно решать исходную задачу с помощью симплекс-метода.
