2014-02-12
389
Работа расширения газа.
Работа расширения газа, помещенного в рабочую камеру, одна из стенок которой представляет собой незакрепленный поршень, в случае его малого перемещения dx, очевидно, имеет следующий вид:
dA=F×dx=p×S×dx=p×dV
Это элементарная работа расширения газа: внутренний параметр р умножается на элементарное изменение внешнего параметра dV. Заметим, что это выражение элементарной работы никак не связано с формой объёма и останется справедливым в случае, например, раздувающегося резинового шарика.
Энергия поляризованной среды, занимающей объем V, как известно из электростатики, имеет вид:
Wэлектр=V×wэлектр=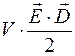
Из двух векторов, характеризующих электрическое поле в среде, вектор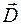 
вдали от границ раздела определяется свободными зарядами, т.е. обстоятельствами внешними по отношению к среде. Сброс энергии, связанный с деполяризацией среды из-за элементарного уменьшения внешнего поля 
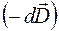, является элементарной работой, совершенной данной средой над окружающими её свободными зарядами, и имеет вид:
|
|
|
,
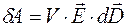где внутренний параметр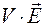 
умножается на элементарное изменение внешнего параметра .
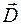3. Работа намагниченной среды, связанная с её размагничиванием.
Энергия намагниченной среды, занимающей объем V, как известно из магнитостатики, имеет вид:
Wмагн=V×wмагн=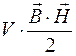
Из двух векторов, характеризующих магнитное поле в среде, вектор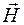 
определяется токами свободных зарядов, т.е. обстоятельствами внешними по отношению к среде. Сброс энергии, связанный с размагничиванием среды из-за элементарного уменьшения внешнего поля 
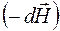, является элементарной работой, совершенной данной средой над окружающими её свободными токами, и имеет вид:
,
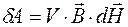где внутренний параметр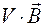 
умножается на элементарное изменение внешнего параметра .
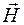Из примеров 1,2,3 можно сделать вывод: элементарная работа рассмотренных равновесных систем выражается через произведение внутреннего параметра на элементарное изменение внешнего. Точно также для произвольной равновесной ТД системы каждому внутреннему параметру Bi системы всегда можно найти сопряженный с ним внешний параметр bi так, что элементарная работа равновесной ТД системы над внешним окружением будет определяться следующим соотношением:
.
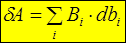Т.е., зная выражение элементарной работы равновесной системы, мы знаем все её параметры. Кстати, до тех пор, пока не написано выражение элементарной работы равновесной системы, нельзя сказать какие параметры являются внешними, а какие – внутренними.
Отсюда более общее определение работы.
Определение: мера обмена энергией между ТД системой и ее окружением в процессе, связанном с изменением внешних параметров системы называется работой А.
|
|
|
Достаточно полно охарактеризовав работу, перейдем к теплообмену.
Определение: процесс обмена энергии, не связанный с механическим движением, называется теплообменом. Более общим определением является следующее: теплообмен – это процесс обмена энергии, не связанный с изменением внешних параметров системы.
Определение: мера передачи энергии в процессе теплообмена называется теплом Q.
#4. Температура.
Заданное ТД состояние определяет все физические величины, связанные с этим состоянием, т.е. функции состояния. Из изложенного выше следует, что состояние не может быть задано одним параметром. Следовательно, функции ТД состояния – это функции нескольких аргументов. Из двух параметров равновесного газа p и V можно искусственным образом сконструировать бесконечное множество функций, физический смысл которых будет неясен или вообще его не будет. Становление термодинамики было связано с открытием функций состояния, имеющих физический смысл. Сейчас мы должны рассмотреть первую важнейшую функцию ТД состояния.
Теплообмен между двумя ТД системами возможен, если их приводят в тепловой контакт. ТД система, которая не находится в тепловом контакте ни с какой другой, называется адиабатически изолированной. Две равновесные системы, приведенные в тепловой контакт друг с другом, могут обмениваться теплом, а могут и не обмениваться. В последнем случае говорят, что они находятся в равновесии друг с другом. Задумаемся: в тепловой контакт могут быть приведены совершенно различные системы, равновесные термодинамические параметры которых никак не связаны друг с другом: они могут отличаться как качественно, так и не совпадать по количеству. И, тем не менее, все системы, находящиеся в тепловом равновесии друг с другом должно что-то объединять. Это что-то должно быть общим в их состояниях.
Для каждой равновесной ТД системы существует функция ее ТД параметров, которая для всех систем, находящихся в равновесии друг с другом, имеет одно и то же значение; эта функция называется температурой.
Таким образом, температура может быть определена только в равновесном состоянии ТД системы. Чтобы понятия «большая» и «меньшая температура» имели строго определенный смысл, необходимо добавить, что при получении телом тепла при постоянных внешних параметрах его температура увеличивается.
Из опыта известен следующий факт: если зафиксировать все внешние параметры системы в термостате, то в ней со временем установится единственно возможный набор равновесных внутренних параметров. Следовательно, в равновесном ТД состоянии все внутренние параметры однозначно определяются внешними параметрами и температурой.
#5. Уравнение состояния.
Соотношения, связывающие температуру и параметры равновесного ТД состояния, называются уравнениями состояния.
Данная масса определенного газа в сосуде в отсутствие внешних полей в состоянии теплового равновесия является ТД системой всего с двумя ТД параметрами: давлением р и объемом V. В термодинамике идеальным газом называется система, уравнением состояния которой является уравнение Менделеева-Клапейрона:
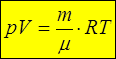
Температура, фигурирующая в этом равенстве, называется идеально-газовой или абсолютной.
Реальным газом определенной массы и определенного химического состава называется система, уравнением состояния которой является уравнение Ван-дер-Ваальса:
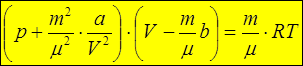
Здесь коэффициенты Ван-дер-Ваальса a и b зависят только от химической природы газа. Температура здесь также является абсолютной.
Физический смысл коэффициентов невозможно прояснить без ссылки на молекулы, из которых состоит газ: а характеризует их притяжение друг к другу, а b - молекулярный объём. Но необходимо отметить, что ТД не "снисходит" до микроскопического строения своих объектов. Понятия "атом", "молекула" не существуют в ТД. В своих построениях этот раздел тепловой физики использует только макроскопические величины, природа которых либо проясняется на основе непосредственного опыта, либо вообще не проясняется никак. ТД является феноменологической наукой.
|
|
|
Кстати, под словом "макроскопическое" нужно понимать нечто соразмерное с человеком и с его органами чувств; то, что воспринимается органами чувств человека непосредственно. Для нашего изложения актуальным является вопрос границы между макроскопикой и микроскопикой. Иными словами, какие макроскопические тела самые малые? Ответ: это объекты, видимые в оптический микроскоп: неживые броуновские частицы и живые биологические клетки. То, что визуализуется с помощью видимого света. К этому можно добавить, что это самые мелкие системы, способные обладать температурой.
