Оценка параметров распределений

· Оценка неизвестного параметра распределения по ограниченной выборке – случайная величина

· Состоятельная, несмещенная и эффективная оценка

· Точечные и интервальные оценки. Доверительные границы и доверительная вероятность

· Неравенство Крамера-Рао:

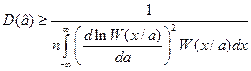
· Оценки математического ожидания и дисперсии нормальной величины

Оценка математического ожидания m.

Минимальная дисперсия оценки

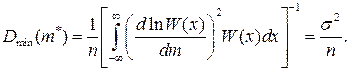
Рассмотрим метод оценки:

.

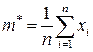Среднее значение оценки:

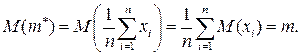
Следовательно, оценка несмещенная.

Дисперсия оценки:

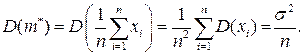
Следовательно, оценка эффективная.

Оценка дисперсии .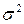

Минимальная дисперсия оценки

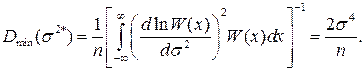
Рассмотрим первый метод оценки – статистическую дисперсию:

.

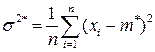Среднее значение оценки:

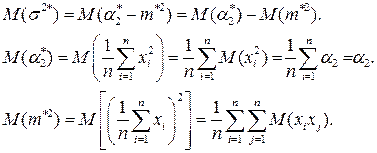
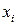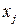и при 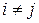независимы, а при 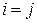- равны, поэтому

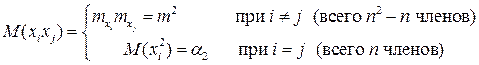
После простых преобразований

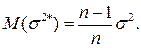
Следовательно, оценка хотя и состоятельная, но смещенная, и смещение тем больше, чем меньше n.

Дисперсия оценки (без вывода):

,

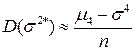то есть может быть меньше, чем 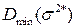- например, при нормальном распределении 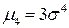. Причина – смещенность оценки, вызывающая дополнительную ошибку оценки дисперсии.

Рассмотрим второй метод оценки:

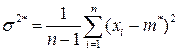
Для этой оценки 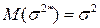, то есть оценка несмещенная. Однако,

,

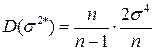следовательно, оценка неэффективная.

Рассмотрим третий метод оценки:

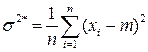
(здесь m не статистическое, а истинное).

Для этой оценки 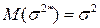, то есть оценка несмещенная, и

,

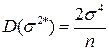следовательно, оценка эффективная.

· Метод моментов оценки параметра: параметр выражается через моменты, а затем вместо моментов подставляются статистические моменты. Пример: равномерное распределение генеральной совокупности в интервале от α до β. Оценить α и β. Решить самостоятельно.

· Метод максимума правдоподобия

· Оценка параметров аппроксимирующих функций методом наименьших квадратов