Проектирование баз данных

Проектирование реляционных баз данных основывается на трех принципах:

- эквивалентных преобразований схемы базы данных.

- уничтожения аномального манипулирования данными

- минимальной избыточности

В общем случае при проектировании ставится задача получения схемы базы дынных, которая эквивалентна и лучше исходной.

В настоящее время известны два подхода к определению понятия эквивалентности схем базы данных: эквивалентность по зависимостям и эквивалентность по данным.

Эквивалентность по зависимостям: схемы содержат одни и те же зависимости: если Г₁ и Г₂ – множества зависимостей двух схем, то эти схемы эквивалентны по зависимостям, если Г₁=Г₂

Эквивалентность по данным: требуется, чтобы обе базы данных содержали одни и те же данные: две БД со схемой Si, i=1,k и Tj, j=1,n соответственно содержат одни и те же данные, если S₁*S₂*…*Sk = T₁*T₂*…Tn, где * - операция естественного соединения отношений.

Одной из целей проектирования реляционных баз данных является уничтожение аномалий манипулирования данными. 3 НФ, введенная ка…ом, позволяет существенно уменьшить(но не исключить) аномалии манипулирования. 3 НФ сохраняет эквивалентность и по зависимостям, и по данным. Каждая НФ либо теряет эквивалентность по данным или по зависимостям, либо допускает аномалии.

Можно дать два определения избыточности: по зависимостям и по данным.

Система отношений S с множеством зависимостей Г избыточна по зависимостям Гi, если

_n _n

(UГj) = (UГj)

^j⁼¹^j⁼¹^j^≠ⁱ

Система S избыточна по данным отношения Si, если S₁*S₂*…*Sk = S₁*S₂*… S_i_-1*S_i₊₁*…*Sn.

Для любого отношения существует такая третья НФ, которая не избыточна по функциональным зависимостям.

В связи с двумя подходами к определению эквивалентных преобразований схем БД существует два метода проектирования схем: синтез и декомпозиция.

Синтез предполагает сохранение эквивалентности по зависимостям.

Декомпозиция – сохранение эквивалентности по данным.

В алгоритмах синтеза достижима только 3НФ, при декомпозиции – любые. При синтезе не снимаются полностью аномалии манипулирования. Можно получить минимальную избыточность по функциональным зависимостям, в алг. декомпозиции – по данным.

Обозначим: A,B,C, …… X,Y,Z – множества атрибутов

a,b,c, …….x,y,z – значения атрибутов

U,R,S - отношения.

Объединение множеств атрибутов X и Y обозначается Х*Y.

Пусть X и Y – атрибуты отношения R.

Атрибут Y функционально зависит от атрибута X, если в каждый момент времени каждому значению х соответствует одно значение y.

X ® Y - Y зависит от X

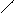X ® Y - зависимости нет.

Если X ® Y и Y ® X, то существует однозначное соответствие.

В каждом отношении имеется определенное множество функциональных зависимостей между атрибутами, причем из одной или нескольких функциональных зависимостей можно вывести другие функциональные зависимости, также присущие этому отношению.

Пример: задано отношение со схемой R (A₁, A₂, A₃)

A₁	A₂	A₃

В отношении R имеются функциональные зависимости

{ A₁® A₂; A₂ ® A₃ }= F

Из анализа отношения очевидно, что в нем, кроме указанных, имеются другие зависимости.

F⁺ ={ A₁® A₃; A₁A₂ ® A₃, A₁A₂A₃_®A₁A₂, A₁A₂_®A₁A₃ }

Заданное множество функциональных зависимостей для схемы отношения R (A₁, A₂, A₃) обозначается через F, а полное множество функциональных зависимостей, которое можно логически получить из множества F, через F⁺. F С F⁺

Чтобы строить множество F⁺ из F, необходимо знать аксиомы вывода одних функциональных зависимостей из других. Аксиомы позволяют вывести полное множество функциональных зависимостей, присущих рассматриваемой схеме отношения R(A₁,……An) по заданному множеству функциональных зависимостей.

Аксиома Ф1 (свойство рефлексивности)

Если Х ≤ U, Y ≤ X, Y ≤ X, то имеет место функциональная зависимость X ® Y. Аксиома Ф1 дает тривиальные зависимости А_j ® A_i

A_i А_j ® А_j

A_i А_j A_kA_eA_r ® А_jA_kA_r и т.д.

Аксиома Ф2 (свойство пополнения)

Если Х ≤ U, Y ≤ U, Z ≤U и задана функциональная зависимость X ® Y, которая либо принадлежит множеству F, либо получена из F с использованием правил вывода, то X*Z®Y*Z

Для аксиомы Ф2 несущественно, перекрываются ли множества X,Y,Z или нет. Используя это правило можно любые атрибуты множества U подставлять одновременно в правую и в левую часть выражения функциональной зависимости, при этом функциональная зависимость сохраняется.

A₁	A₂	A₃	A₄	A₅
и	б	а	в	з
д	и	л	г	з
е	б	м	н	ж
в	к	а	с	х

F={A₁ ®A₂ A₂ ®A₃ A₃ ®A₄ A₄ ®A₅}

Выберем в качестве произвольных множеств атрибутов X,Y и Zследующие множества:

X= { A₁ } Z= { A₄, A₅}

Y= { A₃ }

Кортежи отношения R

XÈZ	YÈZ
< и в з >	< а в з >
< д г з >	< л г з >
< е н ш >	< м н ш >
< в с х >	< а е х >

Приходим к выводу, что существует функциональная зависимость {A₁ A₄ A₅}® {A₃ A₄ A₅} - выполняется свойство пополнения.

Аксиома Ф3 (свойство транзитивности)

Х ≤ U, Y ≤ U, Z ≤ U. Заданы зависимости X {A₁ A₄ A₅} X ® Y, Y ® Z, которые либо принадлежат множеству F, либо получены из F с помощью правил вывода. Следует X ® Z.

Из инфологического проектирования известно, что помимо функциональных существуют многозначные зависимости X ®® Y.

Для того чтобы убедиться, что конкретную взаимосвязь Y (X) можно рассматривать как многозначную зависимость, необходимо выполнить проверку ограничения. Оно состоит в следующем:

Если в отношении R имеет место зависимость X ®® Y, то для двух произвольных кортежей t и s таких, что t[x]=s[x], обязательно отношение содержит кортежи U и V, удовлетворяющие условиям

1) U [X] = V [X] = t [X] = s [X]

2) {U [Y] = t [Y]

U [R-X-Y] = s [R-X-Y]

3) {V [Y] = V [Y]

V [R-X-Y] = V [ R-X-Y]

Задано исходное положение R:

X Y Z

а в с Проверим, существует ли многозначная зависимость Y ®® Z По значению их компонентов формируем кортежи U и V

В отношении R выберем произвольные кортежи t,s, для которых значение атрибута t [Y] = s [Y].

а в д

е ж з

ж в с

ж в д

t: <а, в, с>

s: <ж, в, д>

1) U [Y] = V [Y] = t [Y] = s [Y]= в

2) {U [Z = t [Z] =c

U [R-Y-Z] = s [ R-Y-Z ]= u[X]=s [X]=ш

3) {V [Z] = s[Z]=д

V [ R-Y-Z ] = t [ R-Y-Z ] =VX] =t [X] = а

В отношении должны быть кортежи <ш, в, с> <а, в, д>, что и имеет место в отношении R. Следовательно имеет место многозначная зависимость.

Для многозначных зависимостей существуют также аксиомы вывода:

М1 (аксиома дополнения)

Если имеется набор атрибутов Х ≤ U, Y ≤ U и имеет место многозначная зависимость X®® Y, то имеет место также X®® (U-X-Y)

М2 (аксиома пополнения)

Х ≤ U, Y ≤ U, V ≤ W, X®® Y, отсюда WX ®® VY

М3 (аксиома транзитивности)

Х ≤ U, Y ≤ U, X ®®Y, Y ®® Z: X ®® Z - Y,

Кроме того, существуют аксиомы, связывающие функциональные и многозначные зависимости:

ФМ1

Если Х ≤ U, Y ≤ U и существует X ® Y, то X ®®Y

ФМ2 Если Х ≤ U, Y ≤ U, Z ≤ U, Z ≤ U, W ≤ U, причем W ∩ Y =Æ и X ®® Y, W®Z, то имеет место X® Z.

Система аксиом Ф1-Ф3,М1-М3, ФМ1-2 обладает свойством полноты и надежности.

Свойство полноты означает, что при использовании этих правил можно по заданному множеству исходных зависимостей F= { F₁, F₂, …… F_х} построить все зависимости, принадлежащие множеству F⁺.

Свойство надежности означает, что используя эти правила вывода, можно вычислить только зависимости Fj Î F⁺.

A – множество всех номеров поставщиков

B – множество всех номеров деталей

A*B – п1 д1 кардинальное число

… … S*6 = 30

п1 д6

п2 д1 мощность (степень)

… … n + m

п2 д6

п3 д1

… …

п5 д6