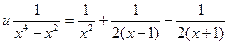а) Разложим знаменатель дроби на множители, решив биквадратное уравнение 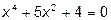 . Получим
. Получим 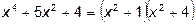 .
.
Для разложения исходной дроби на простейшие используем метод неопределенных коэффициентов,
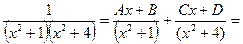
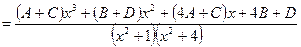 .
.
Приравниваем коэффициенты при равных степенях 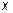 в правой и левой частях этого равенства:
в правой и левой частях этого равенства:
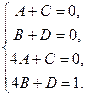
Отсюда
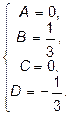 и
и 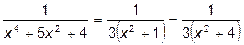 .
.
Тогда
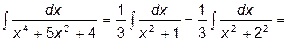
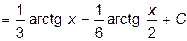 .
.
б) В этом примере корень знаменателя 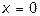 является кратным кратности 2. Поэтому в разложении дроби на простейшие ему будут соответствовать две дроби:
является кратным кратности 2. Поэтому в разложении дроби на простейшие ему будут соответствовать две дроби:
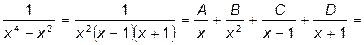
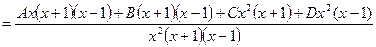
Это равенство должно соблюдаться для любых значений 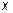 . Вычисления облегчаются, если в качестве таковых взять значения корней знаменателя:
. Вычисления облегчаются, если в качестве таковых взять значения корней знаменателя:
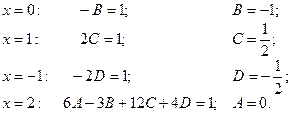
|
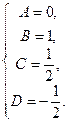
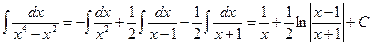 .
.
в) Выделим в числителе дроби производную квадратного трехчлена, а в самом трехчлене - полный квадрат.
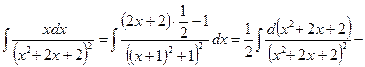
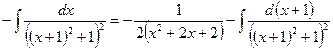
Для нахождения последнего интеграла используем рекуррентную формулу:
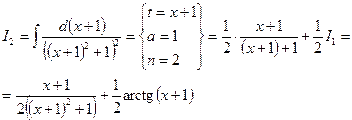
Итак,
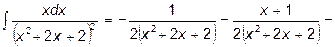
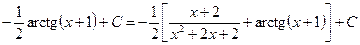 .
.
Задача 6.3. Проинтегрировать тригонометрические функции
а) 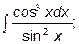 б)
б) 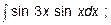 в)
в)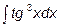 .
.
 2014-02-12
2014-02-12 427
427