578
Микропрограммного устройства и получение функций возбуждения и
Построение обобщенной таблицы возбуждений и выходов
После кодирования состояний памяти МПУ необходимо построить обобщенную таблицу возбуждений и выходов. Таблица строится на основе графа переходов и таблицы входов выбранного элемента памяти.
Таблица содержит строки по числу всех возможных переходов МПУ, отраженных на графе переходов, и столбцы. Количество столбцов задающей части таблицы равно суммарному числу элементов памяти и входных сигналов. Количество столбцов исполнительной части таблицы равно суммарному числу входов элементов памяти и выходов МПУ плюс число элементов памяти. Таблица является обобщенной, так как в нее вносятся не все возможные состояния элементов памяти и входных сигналов, а только те, которые имеют место при переходах МПУ. Остальные состояния в таблицу не вносятся и считаются условными.
Обобщенная таблица возбуждений и выходов МПУ совмещает свойства таблиц возбуждения элементов памяти и переходов-выходов. Для заполнения таблицы необходимо на графе переходов рассмотреть, начиная с начальной вершины, все возможные переходы. В каждую строку обобщенной таблицы возбуждений и выходов заносятся в задающую часть исходное состояние элементов памяти (код вершины) и значение входных сигналов, под влиянием которых происходит переход.
В столбцы исполнительной части каждой строки записывают состояния элементов памяти в t+1 такте (куда идет переход), значения входов элементов памяти, которые необходимы для осуществления данного перехода, взятые из таблицы входов элементов памяти, и значения выходных сигналов на данном переходе.
Построим обобщенную таблицу возбуждений и выходов для примера 5.2. Граф переходов изображен на рисунке 5.12. В качестве элемента памяти примем IK-триггер, таблица входов которого представлена в виде таблицы 5.1. Граф имеет всего 7 различных переходов, значит, таблица должна содержать 7 строк.
МПУ содержит 2 элемента памяти – у1 у2, 3 входных сигнала – х1, х2, х3 и 3 выходных сигнала – z1, z2, z3. Значит, задающая часть таблицы должна содержать пять столбцов – у2, у1, х3, х2, х1, а исполнительная часть должна содержать 9 столбцов – у2 (t+1), y1 (t+1), I2, K2, I1, K1, z3, z2, z1.
Таблица 5.1
| y(t) | y(t+1) | |
| 0~ | 1~ | |
| ~1 | ~0 |
Рассмотрим начальную вершину Y0 графа переходов. Из нее идет 3 перехода: один – в вершину Y1 и два – в вершину Y2. Переход в вершину Y1 происходит при подаче входных сигналов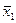 
х2 (т.е. х1 = 0, х2 = 1); при переходе возбуждается выход z2 (т.е. выходные сигналы равны z3=0, z2=1, z1=0) и
МПУ переходит из состояния памяти 00 (у2 = 0, у1 = 0) в состояние 01 (у2 = 0, у1 = 1). По таблице входов IK –триггера определяем, что для перехода элемента памяти у2 из состояния 0 в состояние 0 на него должны быть поданы сигналы 0 ~ (I2 = 0, K2 = ~), а для перехода элемента памяти у1 из состояния 0 в состояние 1 должны быть поданы сигналы I~ (I1 = 1, K1=~).
Вся эта информация заносится в первую строку обобщенной таблицы возбуждений и выходов. В пустых клетках задающей части таблицы проставляем тире.
Аналогичным образом рассматриваем все переходы из всех вершин графа переходов и заполняем все строки таблицы.
Полученная таким образом обобщенная таблица возбуждений и выходов представлена в виде таблицы 5.2.
Таблица 5.2
| y2 | y1 | x3 | x2 | x1 | y2(t+1) | y1(t+1) | J2 | K2 | J1 | K1 | z3 | z2 | z1 |
| -- | ~ | ~ | |||||||||||
| -- | -- | ~ | ~ | ||||||||||
| -- | ~ | ~ | |||||||||||
| -- | -- | ~ | ~ | ||||||||||
| -- | -- | ~ | ~ | ||||||||||
| -- | -- | ~ | ~ | ||||||||||
| -- | -- | ~ | ~ |
Запись значений переменных в задающий части таблицы образует при данной базе обобщенный код (ОК) данной строки.
Например, первая строка (база y2 у1 х3 х2 х1) имеет ОК 00-I0, вторая строка имеет ОК 00--I и т.д.
Таким образом, для каждой переменной исполнительной части таблицы можно записать условия работы (логическую функцию) в виде наборов рабочих и запрещенных, обобщенных кодов. Затем, произведя минимизацию методом поразрядного сравнения ОК можно получить минимальную форму логических функций выходов и возбуждения элементов памяти.
Если символы "-" в ОК заменить переборами значений переменных этих разрядов, то получим полный набор состояний, отвечающих данной строке. Перейдя от двоичного кода к восьмеричному, можно получить набор весовых состояний, соответствующих данной строке при выбранной базе. Например, для первой строки: 00-10=00010v00110=02v06; для второй строки: 00—1=
=00001v00011v00101v00111=01v03v05v07.
Тогда минимизации логических функций можно проводить методом поразрядного сравнения рабочих и запрещенных весовых состояний.
Проведем минимизацию функции J2. Для этого выпишем из обобщенной таблицы возбуждений и выходов рабочие и запрещенные обобщенные коды, расположив их группами (Таблица 5.3).
Таблица 5.3
| y2 | y1 | x3 | x2 | x1 | J2 |
| [0] | -- | -- | [1] | ||
| [0] | -- | [0] | |||
| [1] | -- | -- | [0] | ||
| -- | |||||
| -- | -- |
Сравниваем первый рабочий ОК с запрещенными. Видим, что для отличия от первого запрещенного ОК надо сохранить "I" в разряде х1, а для отличия от второго запрещенного ОК надо сохранить "0" в разряде у1. Обведем их "квадратиками". Значит, из первого рабочего ОК образовался результирующий ОК: – 0 – –1. Сравнивая второй рабочий ОК с запрещенными, получаем результирующий код:– 0 – 0 –, сравнивая третий, получаем –1– –0.
Итак, получили:
J2 (y2 y1 x3 x2 x1) = (- 0 - - 1)v (- 0 – 0 -) v (- 1 - - 0) =
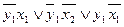
Аналогичным образом минимизируются и остальные функции исполнительной части обобщенной таблицы возбуждений и выходов. Однако при небольшом числе строк обобщенной таблицы нет необходимости для каждой функции выписывать отдельно все рабочие и запрещенные обобщенные коды. Целесообразно минимизацию функций делать прямо по обобщенной таблице возбуждений и выходов.
Проведя минимизацию, получим результирующие коды и алгебраические выражения для всех функций исполнительной части обобщенной таблицы:
К2=1 (запрещенных состояний нет);
К1=1 (запрещенных состояний нет);
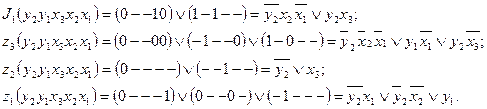
Таким образом, в результате минимизации получили логические функции возбуждения элементов памяти (регистра микрокоманд) и выходов (команд управления):
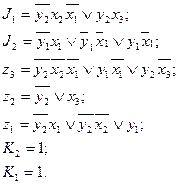
По полученным логическим функциям необходимо построить функциональную схему МПУ.
Построение функциональных схем узлов, реализующих функции возбуждения и функции выходов, в несложных случаях можно проводить обычными способами.
Однако для реальных МПУ системы логических функций возбуждения и выходов содержат десятки и сотни функций, зависящих от десятков и сотен переменных. В связи с этим при построении функциональных схем МПУ надо широко применять методы, позволяющие упростить схемы, - совместную реализацию функций возбуждения и выходов, выявление общих элементов, вынесение за скобки общих частей конъюнкции и т.д.
Имеются и специфичные методы упрощения функциональных схем МПУ, которые применяются в зависимости от конкретных условий решаемой задачи. К этим методам можно отнести раздельное формирование функций возбуждения и выходов, объединенное формирование этих функций, использование дешифратора и преддешифратора и т.д. Мы эти методы не рассматриваем.
Заметим, что не всегда синтезируемый автомат точно укладывается в схему Уилкса. Однако можно указать, что память – это регистр (запоминающее устройство) микрокоманд; схема возбуждения элементов памяти – это формирователь адреса микрокоманд, а схема формирования выходов – это формирователь команд управления.
Если в качестве элементов памяти применяются задержки (Д-триггеры), то вместо функций возбуждения элементов памяти следует получать функции у (t+1). Тогда получим для нашего примера:
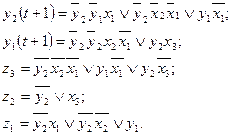
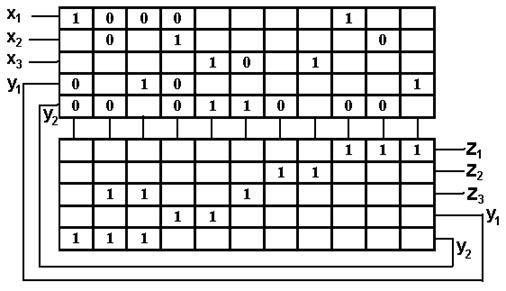
Построим схему такого МПУ с памятью на задержках на ПЛМ (Рисунок 5.16).
|
|
|
|
|
|
|
|
|
|
|
|
|
При построении схемы на ПЛМ с обратными связями (память на задержках) не нужно приводить функции к виду, удобному для построения схемы на элементах И-НЕ, строим ПЛМ сразу по ДНФ.
Можно даже не производить минимизацию ЛФ, брать сразу дизъюнкции конъюнкций рабочих ОК. Однако в этом случае потребуется большее количество вертикальных шин в матрице. Так, для z2 в случае минимизации потребовалось 2 вертикальные шины, а без минимизации понадобилось бы 6 вертикальных шин.
