Геометрическая нелинейность

Нелинейность функции преобразования

Старение” и нестабильность параметров СИ

Причины мультипликативных погрешностей СИ

К причинам возникновения аддитивных погрешностей СИ можно отнести:

- наличие факторов влияния со стороны окружающей среды;

- “старение” и нестабильность параметров ИП.

- нелинейность функции преобразования, связанная с конструкцией прибора.

- токи утечки, обусловленные конечной проводимостью сопротивления изоляции.

Первая причина была рассмотрена выше. Здесь рассмотрим остальные причины.

“Старение ” элементов прибора сводиться к изменению их химических свойств и структуры, которые обусловлены химическими реакциями, протекающими под действием окружающей среды, наличием электрического тока; структурными изменениями, связанными с релаксацией напряжений и диффузией неоднородностей, возникших при изготовлении элементов.

Пример 1. Заготовки для деталей, выполняемых с высокой точностью и стабильностью параметров, выдерживают несколько лет. Также используются и методы искусственного “старения” элементов, например, выдержка деталей при повышенной температуре и влажности.

Пример 2. Если груз подвесить на пружине, то с течением времени длина пружины будет, хотя и медленно, увеличиваться. Это явление называют упругим последействием.

Точно так же, если пружину растянуть на некоторую фиксированную длину и закрепить, то сила упругости, действующая на крепление, будет со временем уменьшаться. Это явление называют релаксацией.

При рассмотрении причин нелинейности функции преобразования СИ необходимо различать геометрическую и физическую нелинейности элементов приборов или прибора в целом.

Пример 1. Зависимость периода колебаний математического маятника от амплитуды колебаний по формуле 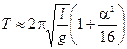– типичное проявление геометрической нелинейности, которая приводит к нелинейности дифференциального уравнения 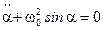колебаний маятника. Эта нелинейность обусловлена зависимостью момента силы тяжести, действующей на маятник, от угла отклонения массы от положения равновесия.

Пример 2. Тело, прижимается к горизонтальной плоскости пружиной. Найдем зависимость проекции F _x(x) силы упругости от перемещения х.

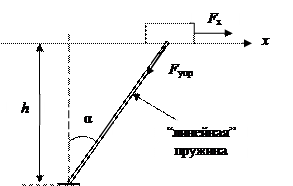Пусть трение отсутствует и пружина - линейная, т.е. 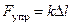, где D l – деформация пружины.

Считаем, что при x =0, F _упр= F ₀, т.е. в положении равновесия пружина натянута. Тогда 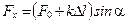, причем .

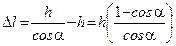Следовательно, 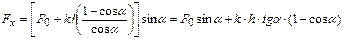. Учитывая, 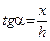, выражая cos a через 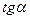, получим .

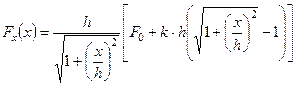Рассмотрим несколько частных случаев (приближений):

Первый случай. Пусть 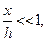тогда, пренебрегая 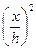, получим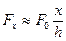

Второй случай (учет слагаемых 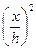).Воспользуемся формуло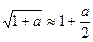й , при 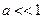. Тогда .

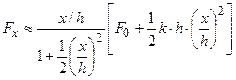Третий случай: начальное натяжение пружины отсутствует, т.е. F ₀=0. Тогда из предыдущей формулы найдем .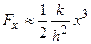

Из полученных формул видно, что результат существенно зависит от используемого приближения, т.е. математической модели. При этом, несмотря на то, что пружина была выбрана линейной, т.е. 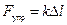, зависимость силы от перемещения может быть существенно нелинейной.