Лямбда-исчисление как формализация функциональных языков

Теория машин Тьюринга является основой императивных языков программирования, лямбда-исчисление служит базисом и математическим «фундаментом», на котором основаны функциональные языки программирования.

Лямбда-исчисление было изобретено в начале 30-х годов логиком А. Черчем, который использовал его в качестве формализма для обоснования математики.

В настоящее время лямбда-исчисление является основной формализацией, применяемой в исследованиях связанных с языками программирования. Это, связано, со следующими факторами:

• Это единственная формализация, которая может быть непосредственно использована для написания программ.

• Лямбда-исчисление дает простую и естественную модель для таких
важных понятий, как рекурсия и вложенные среды.

• Большинство конструкций традиционных языков программирова
ния может быть отображено в конструкции лямбда-исчисления.

• Функциональные языки являются удобной формой синтаксической записи для конструкций различных вариантов лямбда-исчисления. Некоторые современные языки например Haskell имеют полное соответствие своей семантики с семантикой подразумеваемых конструкций лямбда-исчисления.

Лямбда-выражением будем называть конструкцию вида

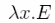
где Е — некоторое выражение, возможно, использующее переменную х. Пример. λх.х² представляет собой функцию, возводящую свой аргумент в квадрат.

Использование лямбда-нотации позволяет четко разделить случаи, когда под выражением вида f(x) мы понимаем саму функцию f, а когда ее значение в точке х.

Применение функции f к аргументу х мы будем обозначать как f х. Будем считать, что применение функции к аргументу ассоциативно влево, т.е. f х у означает (f (x))(y). В качестве сокращения для выражений вида λx. λy. Е будем использовать запись λху.Е (аналогично для большего числа аргументов). Будем считать, что «область действия» лямбда-выражения простирается вправо насколько возможно, т.е., например, λх.х у означает λх. (ху), а не (λх.х) у.

Существует операция каррирования, позволяющая записывать функции многих переменных в обычной лямбда-нотации. Она заключается в том, чтобы выражения вида λх у.х + у рассматривать как функцию 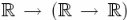, т.е. если его применить к одному аргументу, результатом будет функция, которая принимает другой аргумент. Таким образом:

(λх у.х + у)12 = (λу.1 + у) 2 = 1 + 2.

Переменные в лямбда-выражениях могут быть свободными и связанными. В выражении вида х² + х переменная х является свободной; его значение зависит от значения переменной x ив общем случае ее нельзя переименовать. В подвыражении переменная может быть свободной, в то время как во всем выражении она может быть связана какой-либо операцией связывания переменной, такой как операция суммирования. Та часть выражения, которая находится «внутри» операции связывания, называется областью видимости переменной.

В лямбда исчислении выражения λх.Е [ х ]и λу.Е [ у ]считаются эквивалентными (это называется α -эквивалентностью, и процесс преобразования между такими парами называют α -преобразованием). При этом, необходимо наложить условие, что у не является свободной переменной в Е [ х ].