Уравнения состояния. Определение начальных условий.
Из схемы до коммутации:
ННУ 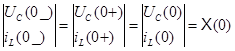
 1
1 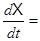 A1X+ B1V
A1X+ B1V
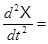 A1
A1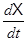 + B1
+ B1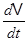
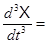 A1
A1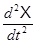 + B1
+ B1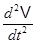 и т.д.
и т.д.
t=0
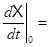 A1X(0)+ B1V(0) V(t)=const
A1X(0)+ B1V(0) V(t)=const 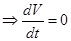
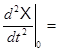 A1
A1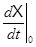 + 0
+ 0
I, E – const X(t)=X уст+X св
a) X уст-? t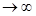
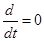
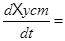 A1Xуст+B1V=0
A1Xуст+B1V=0
X уст=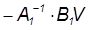
для нашего примера:
X уст=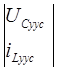 =
=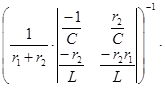
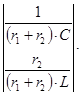 E
E
Или из схемы:
 r1
r1
Ucуст iL уст Ucуст=E
E r2 i L уст=0
б) X св-? V=0
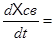 A1Xсв
A1Xсв 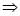
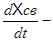 A1Xсв=0
A1Xсв=0
Заменим: 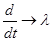
Тогда: 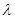 X св-A1Xсв=0
X св-A1Xсв=0
(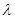 1-A1)Xсв=0
1-A1)Xсв=0
det(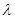 1-A1)=0
1-A1)=0
В нашем примере:
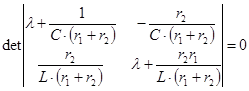
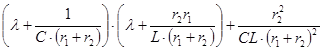 =0
=0
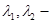 <0 и различные
<0 и различные
Общие уравнения:
X(t)=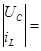
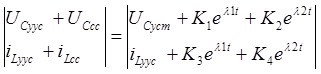
2  X(0)=
X(0)=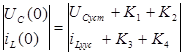
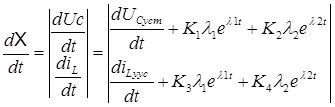
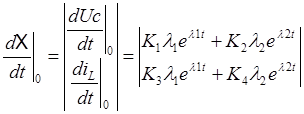
решаем 2 и 3, и находим 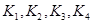
Ответ: Uc(t)=E+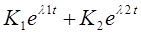
i L(t)=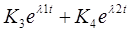
Переходные процессы (динамические режимы) в цепях синусоидального тока и напряжения.
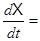 A1X(t)+ B1V(t)
A1X(t)+ B1V(t)
V(t)=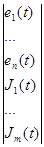 ek(t)=Ekmsin(wt+yk) Jp(t)=Epmsin(wt+yp)
ek(t)=Ekmsin(wt+yk) Jp(t)=Epmsin(wt+yp)
X(t)=Xуст+Xсв Xсв не есть функция от источников и находится также, как раньше.
Для расчёта Хуст можно использовать комплексный метод расчёта, при условии, что все токи и напряжения в цепях изменяются по одному синусоидальному закону с одинаковой w.
e(t)=Emsin(wt+y) 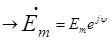 и
и 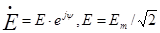
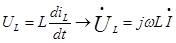
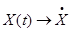 и
и 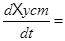 jwXуст
jwXуст



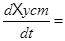 A1Xуст+B1V
A1Xуст+B1V

 jwXуст =A1Xуст+B1V
jwXуст =A1Xуст+B1V

 (jw1-A1)Xуст=B1V
(jw1-A1)Xуст=B1V
Xуст=(jw1-A1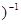 B1V
B1V
 Xуст=
Xуст=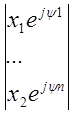
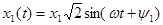 и т.д.
и т.д.
Х1(t)= X1уст+X1св=X1уст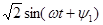 +
+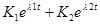
 2014-02-13
2014-02-13 311
311







