Таблица 1.
| Годы | Валовый сбор хлопка-сырца, млн. т. | Скользящая средняя по 5 уровням |
| 4,3 | — | |
| 4,5 | — | |
| 4,3 | 4,72 | |
| 5,2 | 5,00 | |
| 5,3 | 5,30 | |
| 5,7 | 5,64 | |
| 6,0 | 5,78 | |
| 6,0 | 5,86 | |
| 5,9 | 6,10 | |
| 5,7 | 6,32 | |
| 6,9 | 6,58 | |
| 7,1 | 6,94 | |
| 7,3 | 7,48 | |
| 7,7 | 7,68 | |
| 8,4 | 7,92 | |
| 7,9 | 8,22 | |
| 8,3 | 8,38 | |
| 8,8 | 8,54 | |
| 8,5 | 8,94 | |
| 9,2 | 9,18 | |
| 9,9 | 9,30 | |
| 9,6 | — | |
| 9,3 | — |
На рис. 1 показан график, построенный по данным о валовом сборе хлопка-сырца в стране за ряд лет наблюдения и по расчетным данным, представленным в таблице 1.
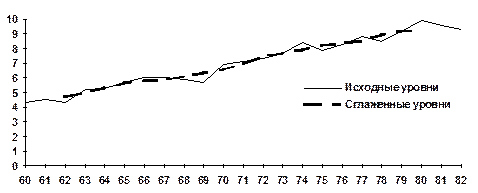
Рис. 1. Валовый сбор хлопка - сырца
Наиболее совершенным способом определения тенденции развития в ряду динамики является метод аналитического выравнивания. При этом методе исходные уровни ряда динамики 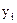 заменяются теоретическими или расчетными
заменяются теоретическими или расчетными 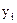 , которые представляют из себя некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Чаще всего в качестве такой функции выбирают прямую, параболу, экспоненту и др.
, которые представляют из себя некоторую достаточно простую математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Чаще всего в качестве такой функции выбирают прямую, параболу, экспоненту и др.
Например, 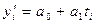 ,
,
где 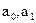 - коэффициенты, определяемые в методе аналитического выравнивания;
- коэффициенты, определяемые в методе аналитического выравнивания;
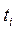 - моменты времени, для которых были получены исходные и соответствующие теоретические уровни ряда динамики, образующие прямую, определяемую коэффициентами
- моменты времени, для которых были получены исходные и соответствующие теоретические уровни ряда динамики, образующие прямую, определяемую коэффициентами 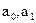 .
.
Расчет коэффициентов 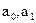 ведется на основе метода наименьших квадратов:
ведется на основе метода наименьших квадратов:
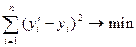

Если вместо 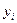 подставить
подставить 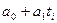 (или соответствующее выражение для других математических функций), получим:
(или соответствующее выражение для других математических функций), получим:
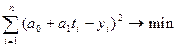
Это функция двух переменных 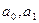 (все
(все 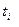 и
и 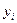 известны), которая при определенных
известны), которая при определенных 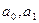 достигает минимума. Из этого выражения на основе знаний, полученных в курсе высшей математики об экстремуме функций n переменных, получают значения коэффициентов
достигает минимума. Из этого выражения на основе знаний, полученных в курсе высшей математики об экстремуме функций n переменных, получают значения коэффициентов 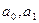 .
.
Для прямой:
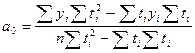
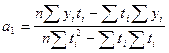
где n — число моментов времени, для которых были получены исходные уровни ряда 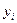 .
.
Если вместо абсолютного времени 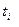 выбрать условное время таким образом, чтобы
выбрать условное время таким образом, чтобы 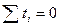 , то записанные выражения для определения
, то записанные выражения для определения 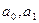 упрощаются:
упрощаются:
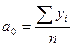
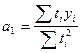
 2015-01-21
2015-01-21 622
622








