Для решения задач линейного программирования был предложен симплекс-метод, разработанный в 1947-1949 гг. американским математиком Дж. Данцигом. Идея состоит в целенаправленном переборе вершин многогранника допустимых решений (опорных планов) в направлении «улучшения» значений целевой функции.
Допустимым решением (допустимым планом) задачи ЛП, данной в стандартной форме, называется упорядоченное множество чисел (х1, х2, …, хn), удовлетворяющих ограничениям; это точка в n -мерном пространстве. Множество допустимых решений образует область допустимых решений (ОДР) задачи ЛП. ОДР представляет собой выпуклый многогранник (многоугольник).
Базисным называется решение, при котором все свободные переменные равны нулю. Опорное решение - это базисное неотрицательное решение. Опорное решение может быть невырожденным и вырожденным. Опорное решение называется невырожденным, если число его ненулевых координат равно рангу системы, в противном случае оно является вырожденным.
Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным и обозначается 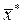 .
.
Симплекс-метод - это универсальный метод решения задач ЛП, представляющий собой итерационный процесс, который начинается с одного решения и в поисках лучшего варианта движется по угловым точкам области допустимых решений до тех пор, пока не достигнет оптимального значения. Алгоритм реализации симплекс-метода сводится к поэтапному пересчету числовых значений компонент очередного анализируемого промежуточного решения (вектора  ) и проверки его на оптимальность. Результаты каждого этапа пересчета записываются в специальные таблицы (симплекс-таблицы).
) и проверки его на оптимальность. Результаты каждого этапа пересчета записываются в специальные таблицы (симплекс-таблицы).
Рассмотрим следующую задачу линейного программирования стандартного вида:
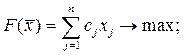 (3.4)
(3.4)

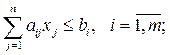 (3.5)
(3.5)
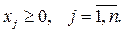 (3.6)
(3.6)
Для применения симплекс-метода ограничения задачи ЛП должны быть приведены к каноническому виду, т.е. система ограничений должна быть представлена в виде уравнений.
Алгоритм симплекс-метода
Шаг 1. Определение исходного опорного плана и составление симплекс-таблицы проходит в два этапа:
а) если ограничения (3.5) имеют тип «≤», то вводим дополнительные неотрицательные переменные. Вектор-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными.
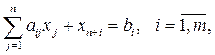 (3.7)
(3.7)
где xn + i – базисные переменные,  ;
;
xj – свободные переменные (небазисные), 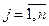 .
.
Решим систему (3.7) относительно базисных переменных:
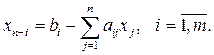 (3.8)
(3.8)
Чтобы решить систему (3.8), полагаем свободные переменные равными нулю: х1 = х2 =... = хn = 0. Имеем:
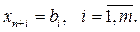 (3.9)
(3.9)
Тогда исходный опорный план будет выглядеть следующим образом: 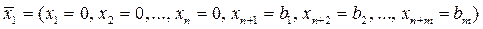 .
.
б) если исходная задача линейного программирования дана в каноническом виде, то базис выбираем из имеющихся переменных.
Базисная переменная - это переменная, встречающаяся только в одном из ограничений с коэффициентом 1 (или который можно привести к коэффициенту, равному 1).
Если нет естественных базисных переменных, вводятся искусственные переменные и переходят к М-задаче.
Составим исходную симплекс-таблицу для случая а). Решение приведено в таблице 3.1.
Таблица 3.1
| ci | БП | c1 | c2 | … | cn | cn+1 | cn+2 | … | cn+m | bi |
| x1 | x2 | … | xn | xn+1 | xn+2 | … | xn+m | |||
| cn+1 | xn+1 | a11 | a12 | … | a1n | 1 | 0 | … | 0 | b1 |
| cn+2 | xn+2 | a21 | a22 | … | a2n | 0 | 1 | … | 0 | b2 |
| … | … | … | … | … | … | … | … | … | … | … |
| cn+m | xn+m | am1 | am2 | … | amn | 0 | 0 | … | 1 | bm |
| Dj | D1 | D2 | … | Dn | 0 | 0 | … | 0 | 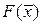
|
Дадим описание этой таблицы и укажем порядок заполнения:
1) в первой строке сj проставляются значения коэффициентов целевой функции при переменных канонической задачи;
2) заполняются столбцы х1, х2,..., xn+m. В них заносятся коэффициенты ограничений канонической задачи, стоящие при переменных xj образующие ее матрицу А;
3) определяются базисные переменные хi и записываются в столбец БП;
4) в столбец bi заносятся значения базисных переменных;
5) в столбец сi записываются коэффициенты целевой функции при базисных переменных;
6) для перехода к следующему опорному решению, рассчитываются Dj – оценочные коэффициенты переменных
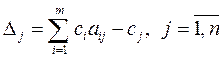 . (3.10)
. (3.10)
В первой симплекс-таблице строка оценок (индексная строка) заполняется коэффициентами целевой функции, взятыми с противоположными знаками;
7) для ячейки  вычисляется значение целевой функции, соответствующее опорному плану
вычисляется значение целевой функции, соответствующее опорному плану
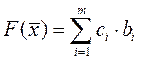 . (3.11)
. (3.11)
Шаг 2. Проверка исходного опорного плана на оптимальность.
Решение задачи ЛП будет оптимальным, если все оценки свободных переменных неотрицательные (т.е. Dj > 0) для задач на максимум и неположительные (т.е. Dj < 0) для задач на минимум. Если условие оптимальности не выполняется, то решение не является оптимальным и его необходимо улучшить, перейдя к новому плану, которому соответствует большее (меньшее) значение целевой функции.
Шаг 3. Определение разрешающего (ключевого) столбца и разрешающей (ключевой) строки.
Из отрицательных оценок (для задач на максимум) или положительных оценок (для задач на минимум) выбираем наибольшую по абсолютной величине оценку:
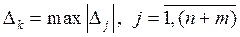 . (3.12)
. (3.12)
Она будет определять разрешающий столбец (с номером k), который показывает, какая переменная на следующей итерации перейдет из свободных в базисные переменные.
Далее определяем минимальное симплексное отношение:
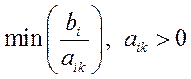 . (3.13)
. (3.13)
Если этот минимум – конечное число, то строка, где этот минимум достигается, называется разрешающей (с номером s). Она определяет ту переменную, которая на следующей итерации выйдет из базиса и станет свободной. Если конечный минимум достигается в нескольких строках, то за разрешающую строку можно принять любую из них. При этом в новом опорном плане значения некоторых базисных переменных с помощью преобразований станут равны 0, т.е. будет получен вырожденный опорный план.
Элемент симплекс-таблицы ask, находящийся на пересечении разрешающих столбца и строки, называется разрешающим элементом.
Шаг 4. Построение нового опорного плана.
Переход к новому плану осуществляется в результате пересчета симплекс-таблицы.
Правила формирования новой симплекс-таблицы:
1) в столбцах «БП»и «ci» в s -й строке записываем xk и ck
2) в столбцах, соответствующих базисным переменным, проставляем нули и единицы: 1 - против «своей» базисной переменной; 0 - против «чужой» базисной переменной; 0 в последней строке для всех базисных переменных;
3) новую строку с номером s получаем из старой делением на разрешающий элемент ask:
 . (3.14)
. (3.14)
4) все остальные элементы новой таблицы вычисляем по правилу «прямоугольника»:
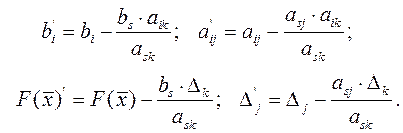 (3.15)
(3.15)
Шаг 5. Выполнение шага 2. И так далее, пока не будет найдено оптимальной решение.
При решении задач ЛП симплексным методом возможны следующие варианты, характеризующиеся определенными признаками:
1) признак альтернативности решения (задача имеет бесконечное множество оптимальных планов) - в симплексной таблице среди оценочных коэффициентов Dj небазисных переменных есть нулевые;
2) признак вырожденности решения – в симплексной таблице хотя бы один из свободных членов равен нулю;
3) признак неограниченности целевой функции (целевая функция не ограничена на области допустимых решений) – в разрешающем столбце среди aik отсутствуют строго положительные элементы;
4) признак несовместности системы ограничений – в симплексной таблице все элементы одной из строк, кроме свободного члена, отрицательные.
.
ПОСТАНОВЛЕНИЕ МЕЖПАРЛАМЕНТСКОЙ АССАМБЛЕИ ГОСУДАРСТВ - УЧАСТНИКОВ
 2014-10-30
2014-10-30 330
330







