Двумерный нормальный закон распределения

Определение. Случайная величина 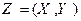называется распределенной по двумерному нормальному закону с параметрами 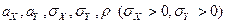, если ее плотность распределения имеет вид:

,

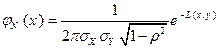где

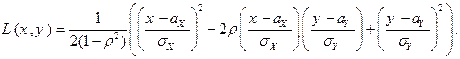
Теорема. Пусть двумерная случайная величина 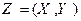имеет двумерный нормальный закон распределения. Тогда корреляционные зависимости между X и Y – линейны:

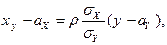
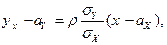
где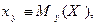

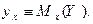
Это важное свойство двумерного нормального закона будет использовано нами позже при рассмотрении теории корреляции.