2015-01-30
759
На базах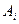 
имеется однородный груз в количестве 
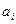тонн. Этот груз требуется перевезти в пункты 
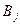, имеющие потребности 
тонн. Расстояние между пунктами отправления и пунктами назначения заданы матрицей расстояний 
.
Стоимость перевозки пропорциональна количеству груза и расстоянию, на которое этот груз перевозится.
Спланировать перевозки так, чтобы их общая стоимость была минимальной (ввиду пропорциональности затрат количеству груза и расстоянию, для решения задачи достаточно минимизировть общий объём плана, выраженный в тонно-километрах).
Задачу решить методом потенциалов, первоначальный опорный план составить методом северо-западного угла.
1. 
.
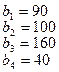
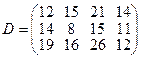2. 
.
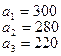
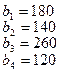
3. 
.
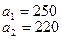
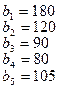
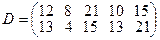4. 
.
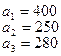
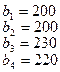
5. 
.
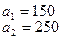
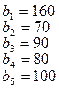
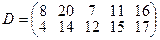6. 
.
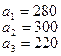
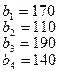
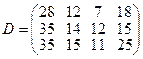7. 
.
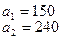
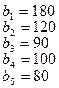
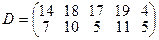8. 
.
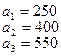
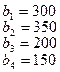
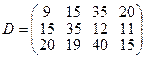9. 
.
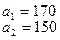
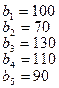
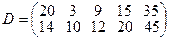10. 
.
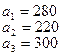
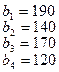
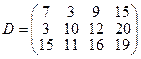11. 
.
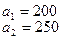
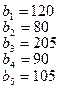
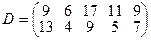12. 
.
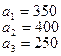
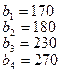
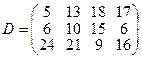13. 
.
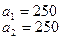
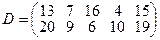14. 
.
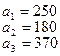
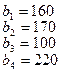
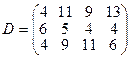15. 
.
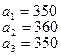
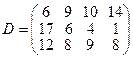16. 
.
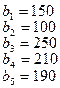
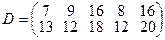17. 
.
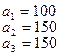
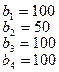
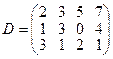18. 
.
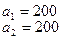
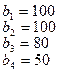
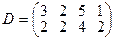19. 
.
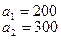
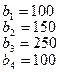
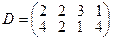20. 
.
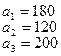
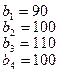
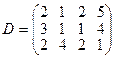21. .
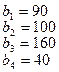
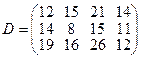22. .
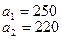
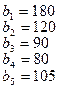
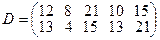23. 
.
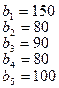
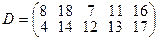24. 
.
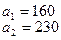
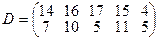25. 
.
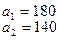
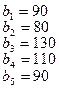
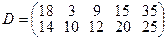26. 
.
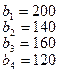
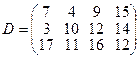27. 
.
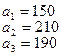
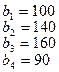
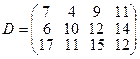28. 
.
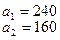
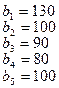
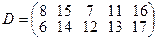29. 
.
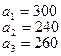
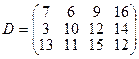30. 
.
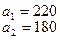
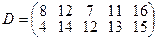ЛИТЕРАТУРА
1. Акулич И. Л.. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986.
2. Высшая математика для экономистов / Под ред. Н. Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.
|
|
|
3. Калихман И. Л. Сборник задач по математическому программированию. – М.: Высшая школа, 1979.
4. Кузнецов Ю. Н., Кузубов В. И., Волощенко А. Б. Математическое программирование. – М.: Высшая школа, 1986.
5. Руководство к решению задач с экономическим содержанием по курсу высшей математики / Под ред. А. И. Карасева и Н. Ш. Кремера. – М.: ВЗФЭИ, 1989.
