Связь потенциальной энергии с работой потенциальных сил. Теорема о кинетической энергии. Закон сохранения полной механической энергии

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы 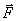, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии 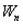. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

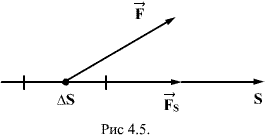
Для установления этой связи вычислим элементарную работу 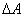, совершаемую силами поля при малом перемещении 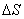тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой 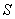. Эта работа равна

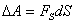
где 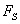- проекция силы 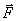на направление .

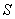Поскольку в данном случае работа совершается за счет запаса потенциальной энергии 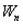, она равна убыли потенциальной энергии 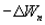на отрезке оси :

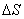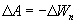
Из двух последних выражений получаем

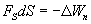
Откуда

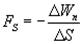
Последнее выражение дает среднее значение 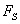на отрезке 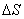. Чтобы

получить значение 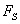в точке нужно произвести предельный переход:

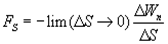
Так как 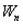может изменяться не только при перемещении вдоль оси 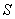, но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от 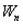по :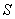

Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

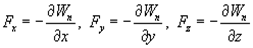
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

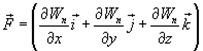
в математике вектор ,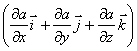

где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом 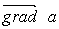.Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком

Кинетическая энергия. Теорема о кинетической энергии.

Рассмотрим тело, к которому приложена постоянная сила 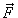(может быть равнодействующей нескольких сил). Об этой силе можно сказать, во-первых, что она сообщает телу ускорение, т. е. изменяет его скорость. Во-вторых, что она совершает работу, потому что тело под действием этой силы перемещается. Поэтому между работой, произведенной силой, и изменением скорости должна существовать связь. Найдем ее.

Рассмотрим простейший случай, когда векторы силы и перемещения направлены вдоль одной прямой в одну и ту же сторону. Направим координатную ось по направлению перемещения тела. Тогда проекции силы 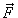, перемещения 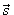, ускорения 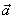и скорости 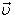будут равны модулям самих этих векторов.

В этом случае выражение для работы силы будет иметь следующий вид:

(1) A = Fs

Из второго закона Ньютона имеем:

(2) F = ma

Известно, что в случае прямолинейного равноускоренного движения перемещение и скорость тела связаны соотношением

(3)

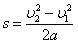
где v₁ и v₂ - модули вектора скорости в начале и в конце участка. Подставив в формулу (1) выражения для F и s из формул (2) и (3), получим:

(4)

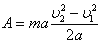
Или

(5)

Формула (5) связывает работу силы А с изменением скорости тела (точнее, квадрата скорости).

Выражение в правой части равенства (5) представляет собой изменение величины 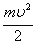- половины произведения массы тела на квадрат его скорости. Эта величина имеет особое название - кинетическая энергия. Из формулы (5) видно, что кинетическая энергия выражается в тех же единицах, что и работа, т. е. в джоулях. Обозначим ее через - E_k. Тогда формула (5) примет вид:

(6) A = E_k2 - E_k1

Работа силы (или равнодействующей сил) равна изменению кинетической энергии тела. Это утверждение называется теоремой о кинетической энергии.

Из теоремы о кинетической энергии следует: кинетическая энергия - это физическая величина, характеризующая движущееся тело; изменение этой величины равно работе силы, приложенной к телу.