Кинетическая энергия

Рассматриваемые вопросы:

Общие теоремы динамики механической системы. Кинетическая энергия: материальной точки, системы материальных точек, абсолютно твердого тела (при поступательном, вращательном и плоском движении). Теорема Кенига. Работа силы: элементарная работа сил, приложенных к твердому телу; на конечном перемещении, силы тяжести, силы трения скольжения, силы упругости. Элементарная работа момента силы. Мощность силы и пары сил. Теорема об изменении кинетической энергии материальной точки. Теорема об изменении кинетической энергии изменяемых и неизменяемых механических систем (дифференциальный и интегральный вид). Потенциальное силовое поле и его свойства. Эквипотенциальные поверхности. Потенциальная функция. Потенциальная энергия. Закон сохранения полной механической энергии.

5.1 Кинетическая энергия

а) материальной точки:

Определение: кинетической энергией материальной точки называется половина произведения массы этой точки на квадрат её скорости:

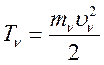(126)

Кинетическая энергия является скалярной положительной величиной.

В системе СИ, единицей измерения энергии является джоуль:

1 дж = 1 Н?м.

б) системы материальных точек:

Кинетическая энергия системы материальных точек это сумма кинетических энергий всех точек системы:

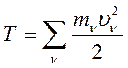(127)

в) абсолютно твердого тела:

1) при поступательном движении.

Скорости всех точек одинаковы и равны скорости центра масс, т.е. 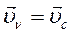, тогда:

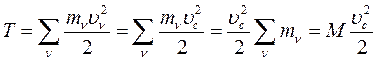(128)

где М – масса тела.

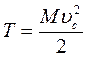(129)

Кинетическая энергия твердого тела, движущегося поступательно, равна половине произведения массы тела М на квадрат его скорости.

2) при вращательном движении.

Скорости точек определяются по формуле Эйлера:

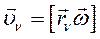(130)

Модуль скорости:

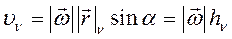(131)

Тогда:

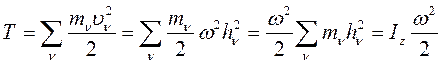(132)

Кинетическая энергия тела при вращательном движении:

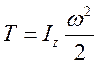(133)

где: z – ось вращения.

Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции этого тела относительно оси вращения на квадрат угловой скорости тела.

3) при плоском движении.

Скорость любой точки определяются через полюс:

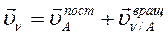(134)

Плоское движение состоит из поступательного движения со скоростью полюса и вращательного движения вокруг этого полюса, тогда кинетическая энергия складывается из энергии поступательного движения и энергии вращательного движения.

Кинетическая энергия через полюс «А» при плоском движении:

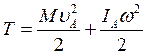(135)

Лучше всего за полюс брать центр масс, тогда:

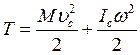(136)

Это удобно потому, что моменты инерции относительно центра масс всегда известны.

Кинетическая энергия твердого тела при плоско-параллельном движении складывается из кинетической энергии поступательного движения вместе с центром масс и кинетической энергии от вращения вокруг неподвижной оси, проходящей через центр масс и перпендикулярной плоскости движения.

Часто бывает удобным брать за полюс мгновенный центр скоростей. Тогда:

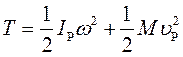(137)

Учитывая, что по определению мгновенного центра скоростей его скорость равна нулю, то .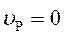

Кинетическая энергия относительно мгновенного центра скоростей:

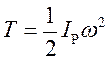(138)

Необходимо помнить, что для определения момента инерции относительно мгновенного центра скоростей необходимо применять формулу Гюйгенса – Штейнера:

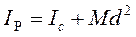(139)

Эта формула бывает предпочтительнее в тех случаях, когда мгновенный центр скоростей находится на конце стержня.

4) Теорема Кенига.

Предположим, что механическая система вместе с системой координат, проходящей через центр масс системы, движется поступательно относительно неподвижной системы координат. Тогда, на основании теоремы о сложении скоростей при сложном движении точки, абсолютная скорость произвольной точки системы запишется как векторная сумма переносной и относительной скоростей:

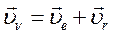(140)

где: 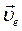- скорость начала подвижной системы координат (переносная скорость, т.е. скорость центра масс системы);

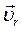- скорость точки относительно подвижной системы координат (относительная скорость). Опуская промежуточные выкладки, получим:

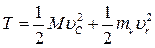(141)

Это равенство определяет теорему Кенига.

Формулировка: Кинетическая энергия системы равна сумме кинетической энергии, которую имела бы материальная точка, расположенная в центре масс системы и имеющая массу, равную массе системы, и кинетической энергии движения системы относительно центра масс.

5.2 Работа силы.

а) Определение: