Однією з важливих характеристик плану щодо певного економічного об'єкта повинен бути рівень гарантії його виконання, або ж обернена величина — ризик невиконання прийнятих зобов'язань. Встановлення плану певного економічного об'єкта (системи) вимагає брати до уваги як внутрішню невизначеність (у характеристиках технологічного процесу), так і невизначеність зовнішнього середовища (постачання сировиною, попит на кінцеву продукцію тощо).
Нехай задані обмеження у загальному вигляді
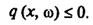 (7.84)
(7.84)
Неможливість, а інколи і недоцільність вимог, щоб рішення задовольняло обмеження (7.84) за будь-яких реалізацій випадкових параметрів 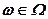 , наштовхує на ідею накладання дещо менш жорстких умов. Замість (7.84) можна допускати невиконання умов з певною ймовірністю:
, наштовхує на ідею накладання дещо менш жорстких умов. Замість (7.84) можна допускати невиконання умов з певною ймовірністю:
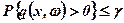 (7.85)
(7.85)
або
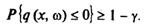 (7.86)
(7.86)
Така ймовірнісна концепція гарантії реалізації плану досить добре відповідає ідеї внесення ризику щодо планування, параметр γ чисельно виражає величину ризику (природно, що у практичних розрахунках недопустимі великі значення γ). Аналогічні модифікації доводиться здійснювати і стосовно функції цілі задачі оптимального планування.
Якщо 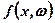 — функція, що виражає ефективність плану при заданих х та ω, то задачу визначення оптимального детермінованого плану х при випадкових параметрах ω доцільно сформулювати в одному з наступних видів:
— функція, що виражає ефективність плану при заданих х та ω, то задачу визначення оптимального детермінованого плану х при випадкових параметрах ω доцільно сформулювати в одному з наступних видів:
а ) max Mf(x, ω) за умов:
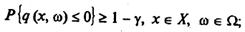
б) max V за умов:
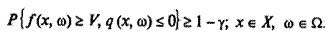 |
Варіант (б) унайбільшій мірі відповідає висунутій ідеї. Його можна трактувати, наприклад, як необхідність граничного підняття значення V, нижче якого ефективність може опуститися лише з малою ймовірністю γ. Цим характеристика ризику поширюється і на оцінку ефективності.
Разом з тим варіант а також є досить раціональним — намагається максимізувати середню (сподівану) ефективність. Перевагою його є те, що він призводить до більш простих у обчислювальному аспекті задач.
Нехай у нас є т обмежень:
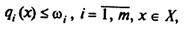 (7.87)
(7.87)
де вектор 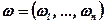 можна інтерпретувати як вектор невизначеного рівня ресурсів.
можна інтерпретувати як вектор невизначеного рівня ресурсів.
Припустимо також, що компоненти ωi вектора ω випадкові і взаємно незалежні, причому задана функція розподілу φi (ωi) кожної i-i компоненти.
Замінимо (7.87) обмеженнями
 (7.88)
(7.88)
Зважаючи на покомпонентну незалежність ωi:
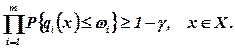 (7.89)
(7.89)
Останню умову можна виразити через функцію розподілу
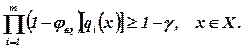 (7.90)
(7.90)
Практично доцільним є і дещо інший підхід, де вимагається виконання наступних обмежень щодо рівнів ризику.
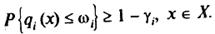 (7.91)
(7.91)
де γi — задані величини ризику (числа). Ці умови перетворюються до виду
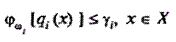
чи
(7.92)
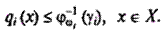
Недоліком цієї постановки задачі є відсутність прямої логічної мотивації у виборі параметрів ризику γ. Однак, можна підпорядкувати, наприклад, вибір γi умові
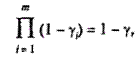 (7.93)
(7.93)
де γ —допустимий ризик (імовірність) порушень усієї системи обмежень.
Приклади обчислення правих частин умов для деяких стандартних розділів.
1. Рівномірний розподіл. Нехай всі ωi розподілені рівномірно
на відрізках
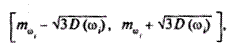
тобто
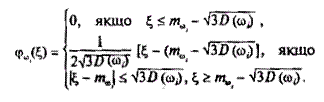
Тоді
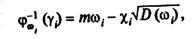 (7.94)
(7.94)
де
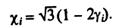 (7.95)
(7.95)
2. Нормальний розподіл. Тут
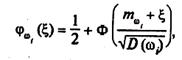
де
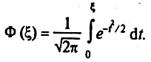
Якщо хi таке, що
 (7.96)
(7.96)
то знову ж таки
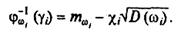 (7.97)
(7.97)
Отже, обмеження в задачі планування повинні ставитися (праві частини), виходячи не з середніх значень ресурсів, а з величин, зменшених відносно середніх пропорційно середньоквадратичним відхиленням 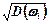 .
.
Якщо задача оптимального планування може бути сформульована як лінійна, де оцінки ресурсів λi (рішення двоїстої задачі), то втрати планової ефективності, що зумовлені невизначеністю, можна наближено оцінити величиною
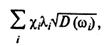 (7.98)
(7.98)
де хi — параметри, що залежать від заданого рівня ризику [формули (7.95) чи (7.96)].
Використовуючи (7.98) можна побудувати графік залежності планових втрат (збитків) від схильності (чи несхильності) суб'єкта прийняття рішень до ризику.
Приклад. Свиноферма має можливість купувати три види зерна та готувати з нього різні суміші для відгодівлі тварин.
Кожен вид зерна містить різну кількість корисних речовин. Припустимо, що до уваги приймаються чотири компоненти речовин А, В, С, D (табл. 7.1).
Таблиця 7.1
| Компоненты | Удельное содержание компонента в зерне i-го вида | ||
| i = 1 | i = 2 | i = 3 | |
| А | |||
| В | |||
| С | |||
| D | 0,6 | 0,25 |
Нехай затрати на 1 кг зерна виду 1, 2 та 3 відповідно становлять 41 тис. крб., 35 тис. крб. та 96 тис. крб. Припустимо, що мінімально допустимі сумарні потреби в компонентах А, В, С, D у сумішах є випадковими величинами ξ1, ξ2, ξ3, ξ4, котрі розподілені рівномірно в інтервалах відповідно [1 000, 1 500], [200, 300], [500, 1 000], [150, 250].
Сформулювати оптимізаційну модель та відшукати оптимальний розв'язок, котрий забезпечував би мінімальні затрати на зерно, при виконанні умов щодо мінімально допустимих потреб в усіх компонентах з ризиком їх невиконання не більшим ніж 20 % (γ = 0,2).
Розв'язання. Позначимо через х1, х2, х3 обсяги зерна відповідного виду, яке необхідно закупити, щоб:
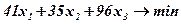 (7.99)
(7.99)
за умов
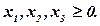 (7.100)
(7.100)
Відповідні ймовірнісні обмеження мають вид
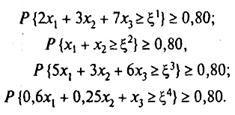 (7.101)
(7.101)
Імовірнісним обмеженням (7.101) будуть відповідати їх детерміновані еквіваленти:
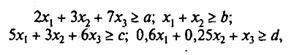 (7.102)
(7.102)
де а — значення випадкової величини ξ1, що задовольняє умові 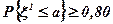 .
.
За умови
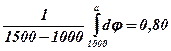 (7.103)
(7.103)
маємо, що а = 1400. Аналогічно визначаються значення b, с, d: b =280; с = 900; d = 230.
Далі, розв'язуючи задачу лінійного програмування (7.99), (7.100), (7.102) симплексним методом, знаходимо, що
x1* = 162,5; x2* = 117,5; х3*= 103,5.
Відповідні оптимальні затрати дорівнюють 20,711 млн. крб.
 2015-01-30
2015-01-30 321
321






