Подобно тому, как для количественного описания поляризации диэлектриков вводилась поляризованность (см. § 88), для количественного описания намагничивания магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:
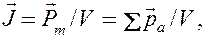
где 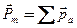 — магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных атомов или молекул (см. (131.6)).
— магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных атомов или молекул (см. (131.6)).
Рассматривая характеристики магнитного поля (см. § 109), мы вводили вектор магнитной индукции 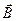 , характеризующий результирующее магнитное поле, создаваемое всеми макро- и микротоками, и вектор напряженности
, характеризующий результирующее магнитное поле, создаваемое всеми макро- и микротоками, и вектор напряженности 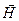 , характеризующий магнитное поле макротоков. Следовательно, магнитное поле в веществе складывается их двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом. Тогда вектор магнитной индукции результирующего магнитного поля в магнетике равен векторной сумме магнитных индукций внешнего поля
, характеризующий магнитное поле макротоков. Следовательно, магнитное поле в веществе складывается их двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом. Тогда вектор магнитной индукции результирующего магнитного поля в магнетике равен векторной сумме магнитных индукций внешнего поля 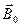 (поля, создаваемого намагничивающим током в вакууме) и поля микротоков
(поля, создаваемого намагничивающим током в вакууме) и поля микротоков 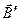 (поля, создаваемого молекулярными токами):
(поля, создаваемого молекулярными токами):
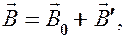 (133.1)
(133.1)
где 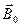 =
= 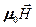 (см. (109.3)).
(см. (109.3)).
Для описания поля, создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечения S и длины l, внесенного в однородное внешнее магнитное поле с индукцией 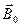 . Возникающее в магнетике магнитное поле молекулярных токов будет направлено противоположно внешнему полю для диамагнетиков и совпадать с ним по направлению для парамагнетиков. Плоскости всех молекулярных токов расположатся перпендикулярно вектору
. Возникающее в магнетике магнитное поле молекулярных токов будет направлено противоположно внешнему полю для диамагнетиков и совпадать с ним по направлению для парамагнетиков. Плоскости всех молекулярных токов расположатся перпендикулярно вектору 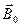 , так как векторы их магнитных моментов
, так как векторы их магнитных моментов 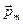 антипараллельны вектору
антипараллельны вектору 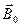 (для диамагнетиков) и параллельны
(для диамагнетиков) и параллельны 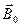 (для парамагнетиков). Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис.189). Нескомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.
(для парамагнетиков). Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются (рис.189). Нескомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.
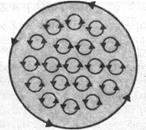
Рис. 189
Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и создает внутри него поле, магнитную индукцию В ' которого можно вычислить, учитывая формулу (119.2) для N = 1 (соленоид из одного витка):
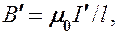 (133.2)
(133.2)
где 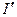 — сила молекулярного тока, l — длина рассматриваемого цилиндра, а магнитная проницаемость
— сила молекулярного тока, l — длина рассматриваемого цилиндра, а магнитная проницаемость 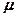 принята равной единице.
принята равной единице.
С другой стороны, 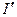 / l — ток, приходящийся на единицу длины цилиндра, или его линейная плотность, поэтому магнитный момент этого тока
/ l — ток, приходящийся на единицу длины цилиндра, или его линейная плотность, поэтому магнитный момент этого тока 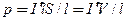 , где V — объем магнетика. Если Р — магнитный момент магнетика объемом V, то P / V — намагниченность магнетика J. Таким образом,
, где V — объем магнетика. Если Р — магнитный момент магнетика объемом V, то P / V — намагниченность магнетика J. Таким образом,
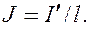 (133.3)
(133.3)
Сопоставляя (133.2) и (133.3), получим, что 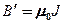 , или в векторной форме
, или в векторной форме
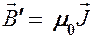
Подставив выражения для 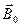 и
и 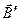 в (133.1), получим
в (133.1), получим
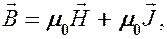 (133.4)
(133.4)
или
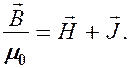 (133.5)
(133.5)
Как показывает опыт, в несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничивание, т. е.
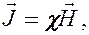 (133.6)
(133.6)
где 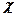 — безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнетиков
— безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнетиков 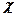 отрицательна (поле молекулярных токов противоположно внешнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с внешним).
отрицательна (поле молекулярных токов противоположно внешнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с внешним).
Используя формулу (133.6), выражение (133.4) можно записать в виде
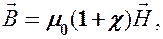 (133.7)
(133.7)
откуда
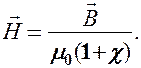
Безразмерная величина
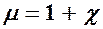 (133.8)
(133.8)
представляет собой магнитную проницаемость вещества. Подставив (133.8) в (133.7), придем к соотношению (109.3) 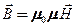 , которое ранее постулировалось.
, которое ранее постулировалось.
Так как абсолютное значение магнитной восприимчивости для диа- и парамагнетиков очень мало (порядка 10-4 — 10-6), то для них (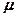 незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков
незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков 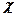 < 0 и
< 0 и 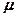 < 1, для парамагнетиков
< 1, для парамагнетиков 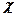 > 0 и
> 0 и 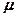 > 1.
> 1.
Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора 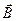 ) является обобщением закона (118.1):
) является обобщением закона (118.1):
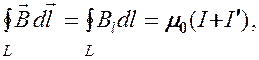
где 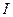 и
и 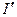 — соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.
— соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.
Таким образом, циркуляция вектора магнитной индукции 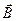 по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор
по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор 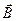 , таким образом, характеризует результирующее поле, созданное как макроскопическими токами в проводниках (токами проводимости), так и микроскопическими токами в магнетиках, поэтому линии вектора магнитной индукции
, таким образом, характеризует результирующее поле, созданное как макроскопическими токами в проводниках (токами проводимости), так и микроскопическими токами в магнетиках, поэтому линии вектора магнитной индукции 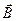 не имеют источников и являются замкнутыми.
не имеют источников и являются замкнутыми.
Можно доказать, что циркуляция намагниченности 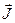 по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:
по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:
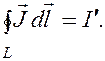
Тогда закон полного тока для магнитного поля в веществе можно записать также в виде
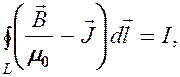 (133.9)
(133.9)
где I, подчеркнем это еще раз, есть алгебраическая сумма токов проводимости.
Выражение, стоящее в скобках в (133.9), согласно (133.5), есть не что иное, как введенный ранее вектор 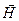 напряженности магнитного поля. Итак, циркуляция вектора
напряженности магнитного поля. Итак, циркуляция вектора 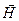 по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром:
по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром:
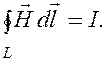 (133.10)
(133.10)
Выражение (133.10) представляет собой теорему о циркуляции вектора 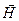 .
.
 2015-01-21
2015-01-21 1755
1755
