И при соединении звездой и треугольником

Активная мощность трёхфазной цепи, в которой нагрузка соединена звездой, определяется через фазные значения напряжения и тока:

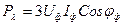. (3.24)

Для активной нагрузки угол сдвига фаз между напряжением и током 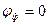, тогда 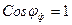. Так как фазное и линейное напряжения соответствуют выражению

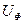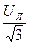= , (3.25)

а фазный ток является линейным, то по закону Ома определим его значение

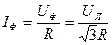, (3.26)

где 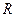- фазное сопротивление нагрузки.

Подставив в формулу (3.24) выражения (3.25) и (3.26), определим активную мощность трёхфазной цепи, соединённой звездой:

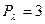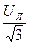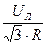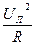∙ ∙ = . (3.27)

Активную мощность трёхфазной цепи, в которой нагрузка соединена треугольником, также можно определить по формуле (3.24). При этом фазное напряжение 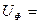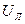, а фазный ток 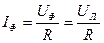, поэтому активную мощность трёхфазной цепи, соединённой треугольником, можно определить по формуле:

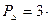
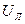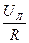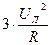∙ = . (3.28)

Используя формулы (3.27) и (3.28), определим коэффициент отношений активных мощностей звезды и треугольника, а также коэффициент их обратных отношений:

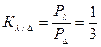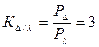; . (3.29)