Определение минимальных форм

Множество Σ_i,входящее в правильную группировку Σ₁, Σ₂,..., Σ_n, будем называть совместимым множеством.

Лемма 7.1. Каждая пара состояний в совместимом множестве должна быть совместимой.

Доказательство. Рассмотрим состояния σ_i1 и σ_i2 из множества 2, правильной группировки Σ₁, Σ₂,..., Σ_n. По теореме 7.1 существует автомат М'', в котором одно состояние, обозначенное σ´_i квазиэквивалентно σ_i1 и σ_i2. Тогда реакции автомата, находящегося в состояниях σ_i1 или σ_i2, на любую входную последовательность ε, допустимую для обоих состояний, должны быть одинаковыми, так как каждая из этих реакций должна быть такой же, как реакция автомата М´| σ´_i на входную последовательность ε. Следовательно, по определению σ_i1 и σ_i2 должны быть совместимы.

В дальнейшем С-множеством автомата М будем называть множество состояний автомата М, которое удовлетворяет двум следующим условиям: (1) каждая пара состояний из С-множества совместима; (2) это множество не является подмножеством другого С-множества, содержащего большее число состояний. Лемма 7.1 тогда позволяет сформулировать следующую теорему.

Теорема 7.2. Каждое множество в правильной группировке автомата М должно быть или С-множеством, или подмножеством С-множества автомата М.

Таким образом, построение минимальной формы может быть выполнено путем перечисления всех возможных С-множеств с последующим формированием всех возможных группировок из перечисленных С-множеств или из подмножеств этих С-множеств. Наименьшая группировка, которая оказывается правильной, является минимальной правильной группировкой и представляет собой минимальную форму данного автомата.

Перечень всех возможных С-множеств может быть легко составлен, когда задан перечень всех совместимых пар. Перечень всех совместимых пар в свою очередь может быть получен из таблицы пар, как описано в § 7.2. Процедура получения всех С-множеств из совместимых пар состоит в следующем.

Алгоритм 7.1. Даны все совместимые пары автомата М; требуется определить все С-множества автомата М. (1) Пусть первый перечень множеств состояний состоит из всех совместимых пар автомата Ж и из отдельных состояний, не принадлежащих ни к одной из совместимых пар. Полагаем k = 2. (2) Для каждого множества состояний { σ_i1, σ_i2,..., σ_ih }, содержащихся в (k — 1)-м перечне, выполняем следующие операции. Определяем l состояний автомата М, скажем σ_j1, σ_j2,..., σ_ji таких, что σ_id (d= 1, 2,..., l) не включено в данное множество, и таких, что каждое σ_id образует совместимую пару с каждым состоянием из этого множества. Заменяем множество { σ_i1, σ_i2,..., σ_ih } l множествами { σ_i1, σ_i2,..., σ_ih, σ_jd }, d=1, 2,..., l. Если l = 0, то заменим множество { σ_i1, σ_i2,..., σ_ih } самим собой. (3) Исключаем из нового перечня множеств все одинаковые множества, оставляя по одному представителю от каждой группы одинаковых множеств, и все множества, являющиеся подмножествами других множеств. Пусть полученный таким образом перечень будет k-n перечнем. (4) (а) Если k-й перечень отличается от (k—1)-го перечня, то увеличиваем k на единицу и возвращаемся к (2). (б) Если k-й перечень совпадает

с (k — 1)-м, то он является перечнем всех С-множеств автомата М.

Выполнение алгоритма 7.1 облегчается построением матрицы совместимости, обозначаемой [С_м], элемент (i, j) которой равен 1, если {σ_i, σ_j } или { σ_j, σ_i}—совместимые пары состояний, и 0 в противном случае. По построению, если в каждой строке σ_i1, σ_i2,..., σ_in содержится 1 в каком-либо данном столбце σ_jd, то σ_jd образует совместимые пары с каждым состоянием из множества (σ_i1, σ_i2,..., σ_ih). Следовательно, если {σ_i1, σ_i2,..., σ_ih }—множество в (k — 1)-м перечне и если строки σ_i1, σ_i2,..., σ_ik матрицы совмещений содержат единицу в столбце σ_jd, множество { σ_i1, σ_i2,..., σ_ih} должно быть заменено множеством {σ_i1, σ_i2,..., σ_ih,σ_jd}.

В качестве примера рассмотрим автомат A32, изображенный на рис. 7.1. В таблице 7.2 получены все совместимые пары автомата A32, из которых может быть составлен первый перечень:

{1,2}, {1,3}, {1.5}, {2.3}, {2,4}, {2,5}, {3,5}, {3.6}, {4,6}.

Матрица совмещений для A32, которая может быть построена непосредственно по первому перечню, представлена выражением (7.1):

Из этой матрицы и первого перечня можно найти второй перечень:

{1, 2, 3}, {1, 2, 5}, {1. 3, 5}, {2, 3, 5}, {2, 4}, {3, 6}, {4. 6}.

Например, обе строки 1 и 2 в (7.1) содержат единицы в столбцах 3 и 5; поэтому множество {1, 2} первого перечня заменяется множествами {1, 2, 3} и {1, 2, 5}. Так как в матрице нет столбцов, в которых обе строки 2 и 4 содержат единицу, то множество {2, 4} из первого перечня заменяется множеством {2, 4}. Из (7.1) и второго перечня можно найти третий перечень: {1, 2,,3, 5}, {2, 4}, {3, 6}, {4, 6}. Так как этот перечень такой же, как и четвертый, то он содержит все С-множества автомата A32.

Минимальная форма A32, а именно A32 соответствует наименьшей правильной группировке, построенной из перечисленных С-множеств или из подмножеств этих С-множеств. Так как каждая группировка должна содержать все шесть состояний, минимальная правильная группировка должна иметь мощность 2 или больше. Однако, так как группировка {1, 2, 3, 5}, {4, 6} не является правильной, нижняя граница мощности, равная 2, недостижима. При помощи таблицы 7.2 можно легко проверить, что {1. 2}, {3, 5}, {4, 6} составляют правильную группировку; поэтому эта группировка и есть минимальная правильная группировка. Можно легко проверить, что {1. 5}, {2, 4} и {3, 6} составляют другую минимальную правильную группировку. Отсюда следует, что минимальная правильная группировка автомата с ограничениями на входе не всегда однозначна. Значит, заданный автомат с ограничениями на входе может иметь несколько минимальных форм, которые не обязательно изоморфны друг другу.

Как только получена минимальная правильная группировка автомата М, может быть получена таблица переходов соответствующей минимальной формы М из таблицы переходов М следующим образом.

Алгоритм 7.2. Дана минимальная правильная группировка автомата М, а именно Σ₁, Σ₂,..., Σ_n, где Σ_i есть {σ_i1, σ_i2,..., σ_ri}; надо построить минимальную форму Ṁ с множеством состояний { σ´₁, σ´₂,..., σ´_n }. (1) Полагаем k=1. (2) (а) Если все клетки в подтаблицах z_v и s_v+1 автомата М, расположенные на пересечении строк σ_k1, σ_k2,..., σ_krk и столбца ξ_j, содержат прочерк, то в Клетках подтаблиц z_v

и s_v+1 автомата М, расположенных на пересечении строки σ´_k и столбца ξ_j, тоже проставим прочерк, (б) Если, по крайней мере, одна из клеток в подтаблице z_v автомата М, расположенных на пересечении строк σ_k1, σ_k2,..., σ_kh и столбца ξ_j, не содержит прочерка, то проставим содержимое таких клеток в клетке, расположенной на пересечении строки σ´_k и столбца ξ_j в подтаблице z_v автомата Ṁ. (в) Если в подтаблице s_v+1 автомата М есть клетки без прочерка, расположенные на пересечении строк σ_k1, σ_k2,..., σ_kh, и столбца ξ_j, то находим совместимое множество Σ_i, в которое включены все элементы, соответствующие этим клеткам. Пусть σ´_i будет содержимым клетки, общей для строки σ´_k и столбца ξ_j в подтаблице s_v+1 автомата Ṁ. (3) (а) Если k < n, то увеличиваем k на 1 и возвращаемся к (2). (б) Если k = n, то таблица переходов для М построена.

Таблица 7.3 представляет собой таблицу переходов автомата A32(с волной) который является минимальной формой автомата A32.

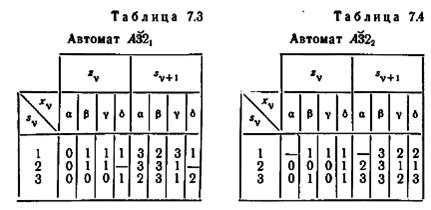
Эта таблица построена на основе минимальной правильной группировки {1, 2}, {3, 5}, {4, 6}. Множества группировки представлены в A32₁ состояниями 1, 2, 3 соответственно. Таблица 7.4 представляет собой таблицу переходов автомата A32₂(с волной), являющегося минимальной формой A32. Таблица построена на основе минимальной правильной группировки

{1,5}, {2,4}, {3,6}, множества которой представлены в A32₂(с волной)

состояниями 1, 2, 3 соответственно.

На рис. 7.2 и 7.3 приведены графы переходов автоматов A32₁(с волной) и A32₂(с волной) соответственно. Для иллюстрации квазиэквивалентности автоматов A32₁(с волной),A32₂(с волной) по отношению к автомату A32

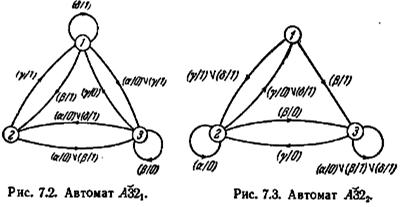
рассмотрим входную последовательность торая допустима для состояния 1 автомата A32. Когда эта γγδαδγαβγαγββδ последовательность прикладывается к A32 в состоянии 1 или к A32₁(с волной) в состоянии 1, или к A32₂(с волной) в состоянии 1 (два последних состояния квазиэквивалентны первому), видно, что реакция автоматов на эту последовательность одинакова у всех автоматов и выражается так: 10101100000111.