2015-02-27
656
К единичным показателям надёжности в соответствии с ГОСТ 27.002-80 относятся показатели безотказности, показатели ремонтопригодности и показатели долговечности.
Рассмотрим количественную оценку данных показателей на следующем примере
Пример 2.
В результате тестовых испытаний программного изделия, состоящего из 10 модулей было получено следующие данные для параметров n,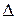 
di, di ( п.3.2):
| Время (t) | t0 | t1=5c | t2=10с | t3=15c | t4=20c |
| параметры | |||||
| n | |||||
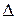| di
| - | ||||
| di | - | ||||
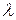
| 0.02 | 0.022 | 0.025 | 0.03 | |
| Pоп | 0.9 | 0.8 | 0.7 | 0.5 | |
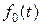
| 0.02 | 0.02 | 0.02 | 0.04 |
Параметры 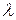, Pоп, 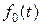определяются по формулам (3.12), (3.5), (3.7) соответственно.
Используя полученные данные можно построить графики функции плотности распределения отказов 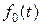, и лямбда-характеристики исследуемого процесса.
Вероятностная оценка показателей надёжности в данном случае может быть, например, следующей.
Сформулируем задачу следующим образом:
а) какова вероятность возникновения хотя бы одного отказа в течении 1 часа испытаний;
б) какова вероятность возникновения двух отказов за 1 час;
в) какова вероятность, что возникнет более 5 отказов в течение 1 часа испытаний
Решение:
По условию задачи - среднее количество ошибок возникающих в единицу времени (параметр интенсивности отказов)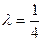 
, время испытаний 
.
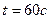а) оценим вероятность не возникновения отказа в течение требуемого интервала времени (воспользуемся формулой распределения Пуассона (2.25):
,
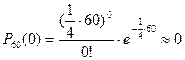Тогда вероятность возникновения хотя бы одного отказа в рассматриваемом промежутке времени:
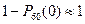
б)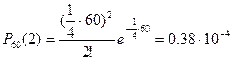 
в) События «возникло менее пяти отказов» и «возникло более пяти вызовов» противоположны, поэтому искомая вероятность того, что за 60 минут произойдёт более 5 сбоев
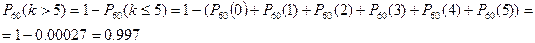
следовательно, вероятность того, что в заданном промежутке времени произойдёт более 5 сбоев очень велика
