Алгоритм Форда-Фалкерсона

Связность и реберная связность стали значительно понятней, а их вычисление значительно проще после установления связей между теорией связности и расчетами потоков в сетях. Выделим в ИВС два узла - источник s и сток t. Если бы это была сеть из труб заданного сечения, можно было бы задать вопросом: какой максимальный поток может перенести эта сеть от s к t?

Пусть узлы n₁, n₂,..., n_k соединены ребрами и задана матрица G=|gij| (1£ i,j£ k) пропускных способностей, соединяющих узел ni с узлом nj, причем в силу дуплексности каналов связи предполагается симметричность матрицы G. Необходимо для каждой пары (ni, nj) определить маршрут, обеспечивающий максимальную пропускную способность. Использование теоремы об (s-t)-разрезе неориентированного графа позволяет сконструировать конечный алгоритм поиска оптимальных потоков.

Согласно теореме Форда-Фалкерсона максимально возможное значение суммарного потока на конечных дугах равно минимальной пропускной способности выбранного разреза. При этом под пропускной способностью разреза понимается сумма пропускных способностей дуг, образующих разрез.

В математической записи соотношение, выражающее содержание теоремы Форда-Фалкерсона, выглядит следующим образом:

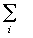
f(v_i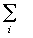,v_j) = c(v_i,v_j),

где f(v_i,v_j) - значение потока по дугам заданного графа; c(v_i,v_j)- пропускная способность дуги; i - все вершины подграфа, образующие разрез; j - дополнение разреза до множества всех вершин графа.

На базе теоремы построен одноименный алгоритм, позволяющий найти минимальные разрезы и оценить соответствующие им значения максимального потока. Принцип, лежащий в основе алгоритма, состоит в том, чтобы найти все возможные насыщенные пути (цепи), ведущие от v_s к v_t для (s-t)-разреза. С этой целью последовательно, начиная с вершины v_s, просматривается множество смежных вершин v_i. Из множества дуг (v_s,v_i), соединяющих vs с v_i, выбирают одну, у которой величина потока ближе всех подходит к значению насыщения. Помечают вершину v_i знаком, показывающим, что она была просмотрена, и приписывают ей величину d, на которую можно увеличить поток по дуге, ведущей в эту вершину. Затем просматривают последующие вершины v_j, смежные с v_i, и останавливаются на той, в которую ведет дуга с потоком, ближайшим к значению насыщения. По этой дуге переходят в соответствующую вершину v_j. Делают отметку и идут далее в направлении вершины v_t. Если путь, на котором будут отмечены все пройденные вершины, приведет в вершину v_t, то это говорит о том, что найден один из путей, наиболее близкий к насыщению. Нужно довести поток по нему до насыщения, увеличивая тем самым поток на графе. Значение, на которое можно увеличить поток, находится как минимальное из всех d, найденных ранее для отмеченных вершин. Для выяснения вопроса, является полученный таким образом поток максимальным или нет, следует просмотреть все другие возможные пути, ведущие от v_s к v_t. Для этого необходимо возвратиться в v_s и повторить описанные выше действия, но идти следует по еще не отмеченным вершинам.

В результате выполнения указанного алгоритма возможны два варианта:

· насыщенный путь снова приводит от v_s к v_t, т.е. удается найти ненасыщенные пути, и, значит, можно увеличить потоки на их дугах;

· в процессе поиска пути обнаруживается вершина, у которой все смежные вершины уже отмечены, и, следовательно, новых путей, ведущих к v_t, больше нет. Это указывает на то, что в ходе выполнения алгоритма был найден максимальный поток.

Такая тесная связь между потоком в сети и ее связностью приводит к результату, известному как теорема Уитни. Эта теорема утверждает, что в графе со связностью n любую пару узлов s и t можно соединить, по крайней, мере n различными цепями, не имеющими общих узлов, кроме s и t. Существует целый ряд подобных теорем, связывающих размеры сечений с числом независимых цепей.