8.1.1–8.1.10. Найти неопределенные интегралы. Результаты проверить дифференцированием.
8.1.1.а) 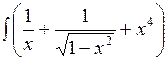 dx; б)
dx; б) 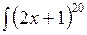 dx;
dx;
в) 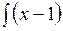 e x dx; г)
e x dx; г) 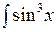 cos5 x dx.
cos5 x dx.
8.1.2.а) 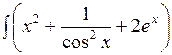 dx; б)
dx; б) 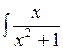 dx;
dx;
в) 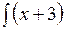 cos x dx; г)
cos x dx; г) 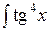 dx.
dx.
8.1.3.а) 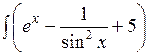 dx; б)
dx; б) 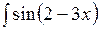 dx;
dx;
в) 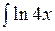 dx; г)
dx; г) 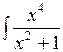 dx.
dx.
8.1.4.а) 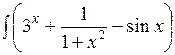 dx; б)
dx; б) 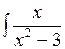 dx;
dx;
в) 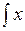 sin x dx; г)
sin x dx; г) 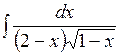 .
.
8.1.5.а) 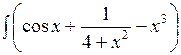 dx; б)
dx; б) 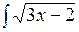 dx;
dx;
в) 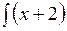 e x dx; г)
e x dx; г) 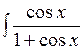 dx.
dx.
8.1.6.а) 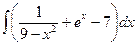 ; б)
; б) 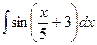 ;
;
в) 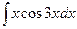 ; г)
; г) 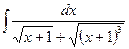 .
.
8.1.7.а) 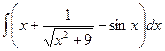 ; б)
; б) 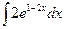 ;
;
в) 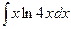 ; г)
; г) 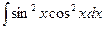 .
.
8.1.8.а) 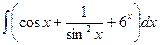 ; б)
; б) 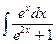 ;
;
в) 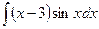 ; г)
; г) 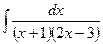 .
.
8.1.9.а) 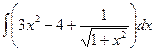 ; б)
; б) 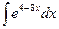 ;
;
в) 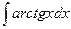 ; г)
; г) 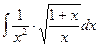 .
.
8.1.10.а) 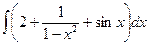 ; б)
; б) 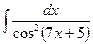 ;
;
в) 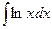 ; г)
; г) 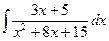 .
.
8.2.31–8.2.40. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
8.2.31. 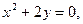
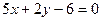 .
.
8.2.32. 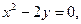
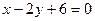 .
.
8.2.33. 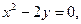
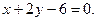
8.2.34. 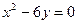 ,
, 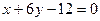 .
.
8.2.35. 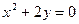 ,
, 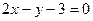 .
.
8.2.36. 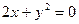 ,
,  .
.
8.2.37. 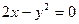 ,
, 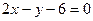 .
.
8.2.38. 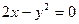 ,
, 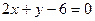 .
.
8.2.39. 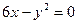 ,
, 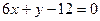 .
.
8.2.40. 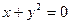 ,
, 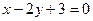 .
.
9.1.11–9.1.20. Найти производные функции двух переменных.
9.1.11. 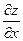 ,
, 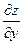 , если
, если 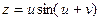 , где
, где 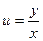 ,
, 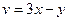 .
.
9.1.12. 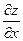 ,
, 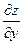 , если
, если 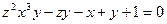 .
.
9.1.13. 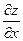 ,
, 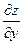 , если
, если 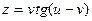 , где
, где 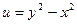 ,
, 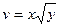 .
.
9.1.14. 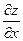 ,
, 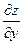 , если
, если 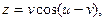 где
где 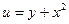 ,
, 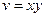 .
.
9.1.15. 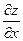 ,
, 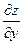 , если
, если 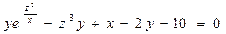 .
.
9.1.16. 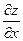 ,
, 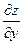 , если
, если 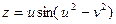 , где
, где 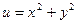 ,
, 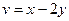 .
.
9.1.17.  , если
, если 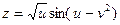 , где
, где 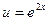 ,
, 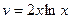 .
.
9.1.18. 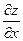 ,
, 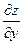 , если
, если 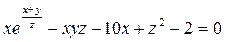 .
.
9.1.19. 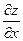 ,
, 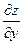 , если
, если 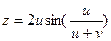 , где
, где 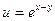 ,
, 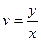 .
.
9.1.20. 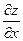 ,
, 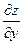 , если
, если 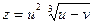 где
где 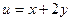 ,
, 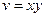 .
.
9.1.51–9.1.60. Расставить пределы интегрирования в повторном интеграле для двойного интеграла 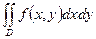 и изменить порядок интегрирования.
и изменить порядок интегрирования.
9.1.51. 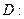
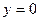 ;
; 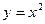 ;
; 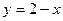 .
.
9.1.52. 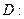
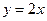 ;
; 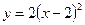 ;
; 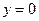 .
.
9.1.53. 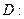
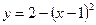 ;
; 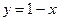 .
.
9.1.54. 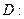
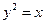 ;
; 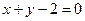 .
.
9.1.55. 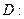
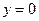 ;
; 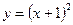 ;
; 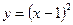 .
.
9.1.56. 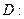
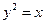 ;
; 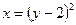 ;
; 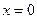 .
.
9.1.57. 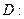
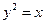 ;
; 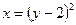 ;
; 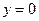 .
.
9.1.58. 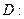
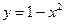 ;
; 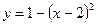 ;
; 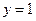 .
.
9.1.59. 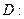
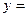 1– х 2;
1– х 2; 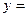 1–(х– 2)2;
1–(х– 2)2; 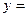 0,5.
0,5.
9.1.60. 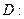
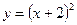 ;
; 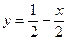 ;
; 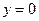 .
.
10.1.1–10.1.10. Вычислить криволинейный интеграл. Сделать чертеж дуги кривой L.
10.1.1. 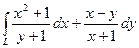 , где L – отрезок прямой от точки (1; 0) до точки (2;1).
, где L – отрезок прямой от точки (1; 0) до точки (2;1).
10.1.2. 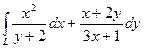 , где L – отрезок прямой от точки (1;1) до точки (2;2).
, где L – отрезок прямой от точки (1;1) до точки (2;2).
10.1.3. 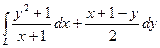 , где L – дуга кривой y = ln(x +1) от точки
, где L – дуга кривой y = ln(x +1) от точки
(0; 0) до точки (e – 1;1).
10.1.4. 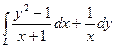 , где L – дуга кривой y = x
, где L – дуга кривой y = x 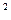 от точки (1;1) до точки (2;4).
от точки (1;1) до точки (2;4).
10.1.5. 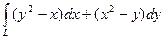 , где L – верхняя половина окружности
, где L – верхняя половина окружности
x = sin 2 t, y = cos 2 t. Интегрировать против часовой стрелки.
10.1.6. 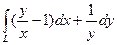 , где L – дуга кривой y = x
, где L – дуга кривой y = x 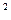 от точки (– 1;1) до точки (– 2; 4).
от точки (– 1;1) до точки (– 2; 4).
10.1.7. 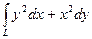 , где L – верхняя четверть окружности x = 2sin t,
, где L – верхняя четверть окружности x = 2sin t,
y = 2cos t. Интегрировать против часовой стрелки.
10.1.8. 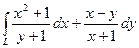 , где L – отрезок прямой от точки (1; 0) до точки (2; 1).
, где L – отрезок прямой от точки (1; 0) до точки (2; 1).
10.1.9. 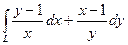 , где L – дуга кривой y = x
, где L – дуга кривой y = x 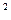 от точки (1; 1) до точки (2; 4).
от точки (1; 1) до точки (2; 4).
10.1.10. 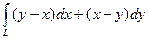 , где L – верхняя половина эллипса x = 3sin 2 t, y = 4cos 2 t. Интегрировать против часовой стрелки.
, где L – верхняя половина эллипса x = 3sin 2 t, y = 4cos 2 t. Интегрировать против часовой стрелки.
 2015-02-04
2015-02-04 692
692







