2015-02-04
503
Рассмотрим неоднородный участок цепи, где действующую э.д.с. на участке 1-2 обозначим как ε 12, а приложенную на концах разность потенциалов – через φ 1– φ 2 (рис.2.2). Если ток проходит по неподвижным проводам, то работа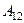 
всех сил (сторонних и электростатических), совершаемая над носителями тока по закону сохранения и превращения энергии, равна теплоте, выделяющейся на участке 1-2.
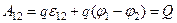
За время t в проводнике выделится количество теплоты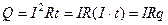 
. Из сравнения этих формул 
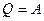, получаем 
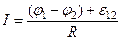. Это выражение представляет собой закон Ома для неоднородного участка, или обобщенный закон Ома.
Если на участке цепи источник тока отсутствует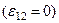 
, то из обобщенного закона Ома получаем закон Ома для однородного участка цепи: 
;
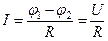Если электрическая цепь замкнута, то Δ φ = 0 (т.к. φ 1 = φ 2), тогда из обобщенного закона Ома следует закон Ома для замкнутой цепи: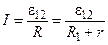 
,
где R – суммарное сопротивление всей цепи, R 1 – сопротивление внешней цепи, r – внутреннее сопротивление источника тока.
