Закон сохранения энергии — не только фундаментальный закон природы, но и эффективный метод решения задач. В этом отношении полезны любые законы сохранения (как принято называть их в механике — интегралы движения), и принцип их использования совершенно универсален — не решая уравнений движения (например, не вычисляя траекторию материальной точки), сразу же связать начальное и конечное состояния системы.
Именно по такому принципу мы выводили формулу Циолковского из закона сохранения импульса.
Начнем с движения материальной точки под действием силы тяжести.
Чтобы использовать закон сохранения энергии для исследования движения, необходимо сначала определить конкретное выражение для потенциальной энергии, то есть найти ее зависимость от положения тела в пространстве. Для этого необходимо выбрать в пространстве некоторую произвольную точку с радиусом-вектором го и вычислить работу, совершаемую силой тяжести при перемещении материальной точки с массой m из заданного положения r в положение r 0.
Чтобы сделать изложенную выше процедуру более наглядной, воспользуемся рис. 5.8.
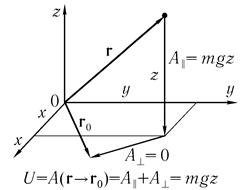
рис 5.8
На этом рисунке положение материальной точки с массой m определяется ее радиусом-вектором r в декартовой системе координат xyz, у которой плоскость хОу совпадает с поверхностью Земли. Для определения потенциальной энергии выберем точку с радиусом-вектором r 0 в любом месте на поверхности Земли. Работу силы тяжести при перемещении из точки г в точку r 0, которая, как мы знаем, не зависит от пути, вычислим вдоль пути, состоящего из двух отрезков: вдоль вертикали до поверхности и далее вдоль произвольной траектории по поверхности до точки с радиусом-вектором r 0.
На первом участке работа равна произведению модуля силы тяжести mg на величину пути до поверхности Земли, т. е. на координату z нашей материальной точки. А на втором участке работа равна нулю, так как здесь сила всюду перпендикулярна перемещению. Таким образом, работа силы тяжести при перемещении материальной точки из положения с радиусом- вектором r в положение с радиусом-вектором r 0, то есть потенциальная
энергия,
U(r) = mgz.
Следовательно, закон сохранения энергии при движении материальной точки под действием только силы тяжести имеет вид следующего соотношения, справедливого для любой точки траектории:
Е = mv2(r)/2 + mgz = const. (5.27)
Если, например, тело начинает падать с некоторой высоты z0 с нулевой начальной скоростью, то из закона сохранения энергии (5.27) легко получить
закон нарастания скорости по мере приближения тела к поверхности:
mgz0= mgz + mv2(z)/2 => v(z) = √(2g(z0 - z)).
Определим выражение для потенциальной энергии и для второго простейшего типа движения материальной точки, рассмотренного в предыдущей главе, - для гармонических колебаний груза по поверхности под действием упругой силы со стороны пружины (см. рис. 4.5, 4.6). В качестве произвольного начального положения с радиусом-вектором r 0 в определении потенциальной энергии используем равновесное положение груза при х = 0. Тогда потенциальная энергия в положении х равна работе упругой силы Fy = -кх
при перемещении материальной точки из положения с координатой х в положение с координатой х = 0: U(x) = kx2/2. Таким образом, закон сохранения полной энергии при гармонических колебаниях материальной точки по поверхности записывается в виде
mv2(x)/2 + кх2/2 = const. (5.28)
С помощью этого соотношения можно решать многие задачи о гармонических колебаниях, не прибегая к интегрированию уравнений движения. Так например, если нам задана начальная скорость груза v0 в положении равновесия х = 0, то из (5.28) легко найти амплитуду x0 возникающих после этого гармонических колебаний. При максимальном отклонении скорость груза, а следовательно и его кинетическая энергия равны нулю. Применяя (5.28) к начальному моменту времени и к моменту, когда достигается максимальное отклонение, получаем
mv02/2 = kx02/2, х0= v0√(m/k).
Особо подчеркнем, что закон сохранения энергии при движении во внешнем силовом поле справедлив только при движении материальной точки под действием сил, постоянных во времени. (В противном случае условие (512) не было бы инвариантно по отношению к выбору траектории r (t)). О таком движении говорят иногда, как о движении в постоянном силовом поле, понимая под словом «поле» пространство, каждой точке которого соответствует вектор действующей в пространстве силы.
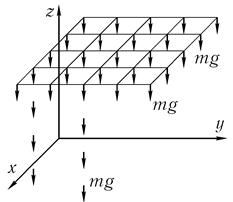
(На рис. 5.9 в качестве примера изображено постоянное силовое поле силы тяжести). Если условие постоянства силового поля не выполняется, полная энергия материальной точки, вообще говоря, не сохраняется.
Полезно рассмотреть также пример, когда для решения задачи используется не охранение энергии, а ее полная диссипация. Это также нередко дает возможность получить простой ответ, не решая уравнений движения.
Уменьшение энергии, обусловленное действием сил трения, можно определить с помощью соотношения между изменением кинетической энергии и работой (5.11), которое часто оказывается полезным при решении задач.
В качестве наглядного примера рассмотрим такую задачу (рис. 5.10). На горизонтальной поверхности лежит тело массы m, которому в начальный момент сообщают скорость поступательного движения v0. Из-за трения о поверхность тело останавливается на некотором расстоянии l от исходного
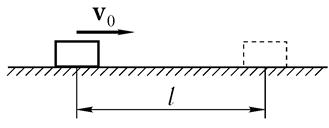
Рис- 5.10
положения. Чему равно это расстояние, если коэффициент трения равен α
Ответ можно, конечно, найти путем решения соответствующего уравнения
движения (второго закона Ньютона). Но решение можно проще и короче
получить с помощью соотношения (5.11), из которого сразу получаем
mv02/2 = FTpl = αmgl, l = v02/(2αg)
Конечно, результат этот приблизителен, а иногда может быть и просто
неверен, поскольку мы воспользовались приближением постоянной силы
трения. Но принцип решения подобных задач наш пример демонстрирует
должным образом.
 2015-02-04
2015-02-04 440
440








