Линейное программирование (ЛП) является одним из разделов математического программирования – дисциплины, изучающей экстремальные (оптимизационные) задачи и разработкой методов их решения.
Оптимизационная задача – это математическая задача, заключающаяся в нахождении оптимального (т.е. максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений (ОДЗ).
В общем виде постановка экстремальной задачи математического программирования состоит в определении наибольшего или наименьшего значения функции 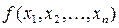 , называемой целевой функцией, при условиях (ограничениях)
, называемой целевой функцией, при условиях (ограничениях) 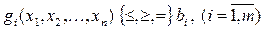 , где
, где 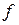 и
и 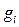 – заданные функции, а
– заданные функции, а 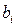 – заданные постоянные величины. При этом ограничения в виде равенств и неравенств определяют множество (область) допустимых решений (ОДР), а
– заданные постоянные величины. При этом ограничения в виде равенств и неравенств определяют множество (область) допустимых решений (ОДР), а 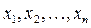 – называют проектными параметрами.
– называют проектными параметрами.
В зависимости от вида функций 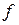 и
и 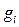 задачи математического программирования делятся на ряд классов (линейной, нелинейное, выпуклое, целочисленное, стохастическое, динамическое программирование и др.).
задачи математического программирования делятся на ряд классов (линейной, нелинейное, выпуклое, целочисленное, стохастическое, динамическое программирование и др.).
В общем виде задача ЛП имеет следующий вид:
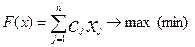 , (5.1)
, (5.1)
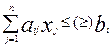 ,
, 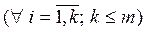 , (5.2)
, (5.2)
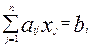 ,
, 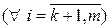 , (5.3)
, (5.3)
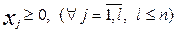 (5.4)
(5.4)
где 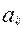 ,
, 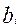 ,
, 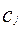 – заданные постоянные величины.
– заданные постоянные величины.
Функцию (5.1) называют целевой функцией; системы (5.2), (5.3) – системой ограничений; условие (5.4) – условием неотрицательности проектных параметров.
Совокупность проектных параметров 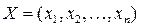 , удовлетворяющих ограничениям (5.2), (5.3) и (5.4), называют допустимым решением или планом.
, удовлетворяющих ограничениям (5.2), (5.3) и (5.4), называют допустимым решением или планом.
Оптимальным решением или оптимальным планом задачи ЛП называется допустимое решение 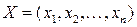 , при котором целевая функция (5.1) принимает оптимальное (максимальное или минимальное) значение.
, при котором целевая функция (5.1) принимает оптимальное (максимальное или минимальное) значение.
Стандартной задачей ЛП называют задачу нахождения максимального (минимального) значения целевой функции (5.1) при условии (5.2) и (5.4), где 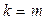 ,
, 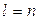 , т.е. т.е. ограничения только в виде неравенств (5.2) и все проектные параметры удовлетворяют условию неотрицательности, а условия в виде равенств отсутствуют:
, т.е. т.е. ограничения только в виде неравенств (5.2) и все проектные параметры удовлетворяют условию неотрицательности, а условия в виде равенств отсутствуют:
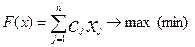 ,
,
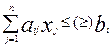 ,
, 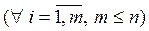 , (5.5)
, (5.5)
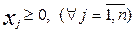 .
.
Канонической (основной) задачей ЛП называют задачу нахождения максимального (минимального) значения целевой функции (5.1) при условии (5.3) и (5.4), где 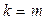 ,
, 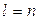 , т.е. т.е. ограничения только в виде равенств (5.3) и все проектные параметры удовлетворяют условию неотрицательности, а условия в виде неравенств отсутствуют:
, т.е. т.е. ограничения только в виде равенств (5.3) и все проектные параметры удовлетворяют условию неотрицательности, а условия в виде неравенств отсутствуют:
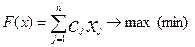 ,
,
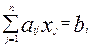 ,
, 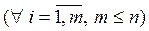 , (5.6)
, (5.6)
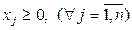 .
.
Каноническую задачу ЛП можно также записать в матричной и векторной форме.
Матричная форма канонической задачи ЛП имеет следующий вид:
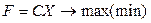 ,
,
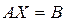 , (5.7)
, (5.7)
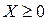 ,
,
где
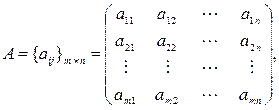
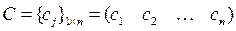 ,
,
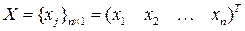 ,
,
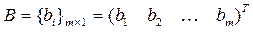 .
.
Векторная форма канонической задачи ЛП:
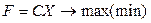 ,
,
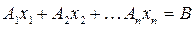 , (5.8)
, (5.8)
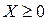 ,
,
где С, X, Ai, B – векторы:
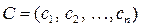 ,
,
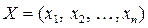 ,
,
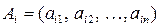 , (
, (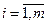 ),
),
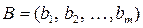 ,
,
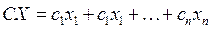 – скалярное произведение векторов C и X.
– скалярное произведение векторов C и X.
Векторное неравенство 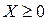 означает, что все компоненты вектора Х неотрицательны, т.е.
означает, что все компоненты вектора Х неотрицательны, т.е. 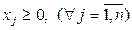 .
.
Все три формы задачи ЛП эквивалентны, т.к. каждая из них с помощью некоторых преобразований может быть переписана в любую форму. При этом необходимо использовать следующие правила:
1. Задачу минимизации функции можно свести к задаче максимизации и наоборот путем замены знаков коэффициентов 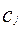 на противоположные, поскольку
на противоположные, поскольку 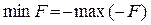 .
.
2. Ограничения-неравенства (5.2) можно заменить эквивалентными ограничениями-равенствами путем введения дополнительных неотрицательных переменных.
Теорема 5.1. Любому решению 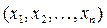 неравенства
неравенства
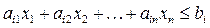 (5.9)
(5.9)
соответствует определенное решение 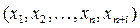 уравнения
уравнения
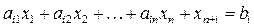 (5.10)
(5.10)
в котором

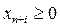 (5.11)
(5.11)
и, наоборот, каждому решению 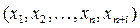 уравнения (5.10) и неравенства (5.11) соответствует определенное решение
уравнения (5.10) и неравенства (5.11) соответствует определенное решение 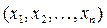 неравенства (5.9).
неравенства (5.9).
Таким образом, если ограничения-неравенства вида 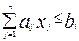 , то можно преобразовать в ограничение-равенство вида
, то можно преобразовать в ограничение-равенство вида 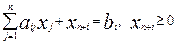 .
.
При ограничении-неравенстве вида 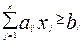 , то можно преобразовать в ограничение-равенство вида
, то можно преобразовать в ограничение-равенство вида 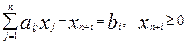 .
.
При переходе от ограничения-равенства к ограничению-неравенству необходимо выразить одну из переменных 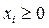 через остальные, затем исключить ее с переходом к неравенству, при этом, если коэффициент при данной переменной +1, то переходим к неравенству вида
через остальные, затем исключить ее с переходом к неравенству, при этом, если коэффициент при данной переменной +1, то переходим к неравенству вида 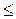 , а если –1, то
, а если –1, то 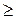 .
.
3. Каждое ограничение-равенство вида 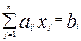 можно записать в виде двух неравенств:
можно записать в виде двух неравенств:
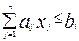 ,
, 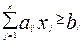 . (5.12)
. (5.12)
4. Переменная 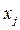 , не ограниченная условием неотрицательности можно заменить разностью двух дополнительных неотрицательных переменных:
, не ограниченная условием неотрицательности можно заменить разностью двух дополнительных неотрицательных переменных:
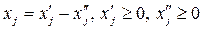 . (5.13)
. (5.13)
 2015-02-04
2015-02-04 1401
1401
