Модального разложения

В рамках МКЭ можно применять метод модального разложения, если рассмотреть задачу о свободных колебаниях стержневой системы, т.е. исключить из уравнения (2.115) вектора узловых сил .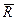

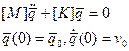(2.116)

Т.к. рассеивание энергии в стержневой системе отсутствует, то можно предположить, что движение всех узлов есть незатухающие гармонические колебания и вектор узловых перемещений представить в виде:

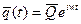
Подставим последнее выражение в (2.116).

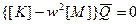(2.117)

Полученная система линейных алгебраических уравнений однородна, если она имеет нетривиальное решение в случае:

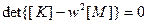(2.118)

Таким образом, решение задачи о свободных колебаниях приводится к обобщенной алгебраической проблеме собственных значений, решение которой дает спектр свободных колебаний.

Собственные частоты – частоты свободных колебаний.

Собственные векторы – формы свободных колебаний или моды.

При составлении программ решения задач динамики МКЭ следует ориентироваться на решение частичной проблемы собственных значений, определяющей младшие (меньшие) частоты свободных колебаний и соответствующие им формы. Общее количество определяемых элементов спектра по литературным данным имеет порядок приблизительно равный 50.

Для решения частичной проблемы собственных значений оптимальным является метод половинного деления с вычисление определителя по схеме Гаусса с полным или частичным выбором ведущего элемента. Для определения собственных форм рекомендуется метод обратных итераций.

Для решения задач динамики вектор узловых перемещений представляется с помощью модального разложения:

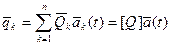
где 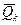- собственные векторы задачи (2.117)

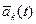- неопределенные коэффициенты

Запишем уравнение (2.115) с право й частью, считая, что векторы

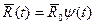
Домножим это уравнение слева на транспонированную матрицу 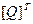и узловые перемещения представим модальным разложением:

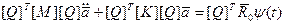
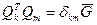
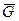- норма

Потребуем, что собственные векторы были нормированы.

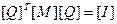
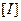- единичная матрица

При условии произведение: 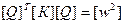становится диагональной матрицей, составленной из квадратов частот свободных колебаний. Приходим к системе несвязанных между собой обыкновенных дифференциальных уравнений второго порядка относительно коэффициентов модального разложения:

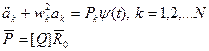(2.119)

Уравнение (2.119) не отличается от полученного ранее уравнения динамики при аналитически определяемых модах колебаний и его решение также записывается в виде интеграла Дюамеля:

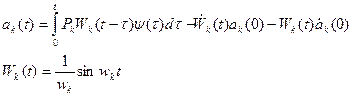
Начальные значения модальных коэффициентов и их скоростей определим следующим образом: запишем модальное разложение начальных условий.

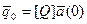
Домножим полученное выражение слева на 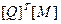, тогда начальные значения модальных коэффициентов определяются так:

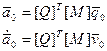(2.120)

Представим узловые перемещения в виде, не содержащим модальных коэффициентов и их начальных значений. Для этого вектор 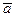представим в следующей форме:

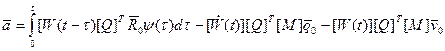
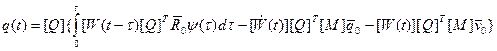(2.121)

Здесь 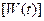- диагональная матрица импульсно-переходной характеристики.

Учитывая, что кроме [W] и 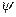в этой формуле ничто не зависит от времени, можно ввести диагональную матрицу реакций на внешние воздействия, каждая компонента которой имеет вид:

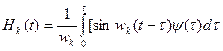(2.122)

Тогда вектор узловых перемещений:

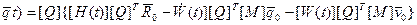(2.123)

Напряжения: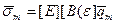

При решении задач о колебаниях стержневых систем с помощью МКЭ следует иметь ввиду, что рекомендованные для статики функции формы (полиномы Эрмита) при решении динамических задач могут дать большие погрешности для частот и форм свободных колебаний. Поэтому естественен принцип разбиения (1 стержень – 1 конечный элемент) нужно использовать с осторожностью. При вычислении некоторых достаточно высоких частот может оказаться необходимым разбивать прямые стержни на несколько конечных элементов.